Hoe de helling onderscheppen vorm (in de algebra) gebruiken

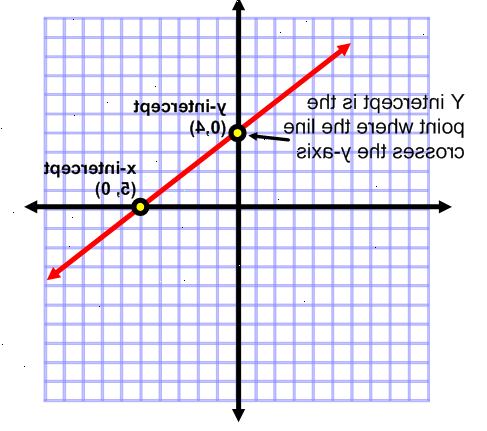
Probleem voor dit artikel

In dit artikel, wordt dit probleem gebruikt om enkele typische stappen laten zien:

1. 1
   Lees dit probleem:
   Uw bankrekening lineair toeneemt elke week. Indien na 20 weken van het werk, uw bankrekening is op 420€, terwijl na 21 weken van het werk is het op 440€ te vinden:
   
   1. De regel die de grootte van uw account heeft betrekking op de tijd, in weken, dat je gewerkt hebt.
      
   2. Het bedrag op uw rekening na 200 weken (bijna vier jaar).
      
   3. Het oorspronkelijke bedrag voordat je begon te werken.
      

   Zie bovenstaand probleem

   1. 1
      Merk op dat in het probleem "uw bankrekening lineair toeneemt per week." betekent dat u opslaat dezelfde hoeveelheid geld elke keer. Dat "glad", uniforme consistente besparingsplan maakt het lineair. Als u niet dezelfde hoeveelheid hele tijd te besparen, dan is het niet lineair (niet glad).
      
   2. 2
      Denk na over y = mx + b die heet de helling y-as vorm van de lineaire vergelijking. Waar 'm' is de helling, "b" is de (b eginning) bedrag in dit soort problemen, genaamd de y-as.
      
      • Als je niet weet dat, de vorm is een ander woord voor een speciaal soort formule die wordt gebruikt als een patroon te volgen. U leert over deze vorm tijdens het gebruik van dit voorbeeld.
   3. 3
      Begin met het zien van welke informatie het probleem voor je heeft. U kunt vinden hoeveel de rekening verhoogt tussen week 20 en 21? Als je dat uit, dan dat u vertelt wat de goede, wekelijkse verandering is:
      
      • Vinden dat door het aftrekken. Wat is 585 minus 560 = ________?
        • Dat geeft ons de snelheid van verandering heet de helling of het kan worden genoemd de groei.
      • Dat is een positieve verandering in x en y en zou een positieve helling en zijn zogenaamde positieve veranderingssnelheid in y omdat het een toename van dit probleem.
        
        • Opmerking: Een ander probleem kan een afnemende hoeveelheid als het doorbrengen van een vast bedrag aan geld elke week van een oude spaarrekening die niet groeit, maar wordt genoemd rottend.
        • Opmerking: Dat verval zou een daling zijn en zou een negatieve snelheid van verandering in y en zou worden genoemd een negatieve helling.
   4. 4
      Welk bedrag zou u hebt opgeslagen sinds u begon te werken?
      
      • Vinden dat voor 20 weken door te vermenigvuldigen: dat de mate van verandering tijden 20 = ________? Doe dat en aftrekken van 560 - ________ = _______ Wat is dat?
      • Dus wat is dan dat deel van de 560 bedrag? U ziet, het is de toegevoegde initiële bedrag dat toevallig in het houden bij de reguliere besparingen begint. Rechts?
   5. 5
      Zien welk bedrag de 20€ mate van verandering zou maken in 21 weken (slechts 25 X 21 = ________)?
      
      • Voeg nu het initiële bedrag dat.
      • Je hebt nu 585. Doe dat te zien.
   6. 6
      Achterhalen die dingen uit en u kunt eenvoudig zien hoeveel was in de rekening (het oorspronkelijke bedrag) voordat u de baan en uw spaarplan begonnen?
      
   7. 7
      Lees het nog eens, als het niet duidelijk, en ook daadwerkelijk de stappen totdat je het... Misschien heb je 'drifting-off "of het luisteren naar iets anders. Algebra zoals de meeste lastige dingen vereist concentratie. Behandel wiskunde als het voor u belangrijk is, en dus aandacht aan te besteden. Alsof het een schat zoeken een klein fortuin waard voor u.

   De oplossingen

   • Zet zinvolle letters (letterlijke symbolen) als een, w, c gebruikt in dit probleem op zijn plaats in de helling y-as formule, en je hebt een regel.
     

   a) Als y = totaal van "account", laten we gebruik maken "a" voor het totaal, en dan x = "weken"
   "C" is een 'vaste' bedrag als een "fixture" of wel "op zijn plaats vast."
   Dus de regel zou worden genoemd een = mw + c.
   Laten we y in plaats van een, en x in plaats van w y =? X +?
   b) Gebruik van de waarde van de snelheid van verandering voor "m" maal 200 voor "w", voeg dan de
   

   Tips

   • Algebra is actief. Je moet de acties (stappen) te doen om te begrijpen hoe alles in elkaar past.
   • Nou ja, niet alleen lezen voorbeelden. Je moet om te schrijven en doe de stappen om de orde en het doel van het proces te betrekken.
   • meet de vertikale versus horizontale verandering in een verhouding. Dit kan samenhangen met de punten of lijnen in een grafiek of een groeisnelheid in de tijd of de helling van een heuvel.

   Maak indruk op je docent

   1. Je kunt je leraar te imponeren door te begrijpen dat bijvoorbeeld je natuurlijk versnellen en vertragen wanneer het reizen - en de grafiek van de snelheid op een reis zou zig-zag. Begrijpen dan dat de gemiddelde koers van de snelheid een rechte lijn zou maken, indien grafiek voor die tegelijkertijd op die reis. Plus, dat is de reden waarom problemen gewoonlijk wordt gebruikt "de gemiddelde snelheid van verandering."
   2. Het is echt indrukwekkend om de leraar wanneer je leren en te begrijpen hoe de lineaire vergelijking van toepassing op allerlei verhaal problemen.
   3. Dit is een echte manier om te laten zien dat u begrijpt: De verandering van y over de verandering van x heet een toename (groei) of een daling (verval) van het verschil van de y gedeeld door het verschil van x. En ook te weten dat het verdelen wordt ook wel een verhouding verval)>. Die verhouding is de snelheid van verandering.
      • Die verhoging of verlaging wordt ook wel de helling of de mate van verandering helling> als mijlen per uur en graag kilometer per seconde, die voorbeelden zijn van een mate van verandering (afstand ten opzichte van de tijd).
      • De helling van een lineaire vergelijking vertegenwoordigt de verandering van y ten opzichte van de verandering van x die vergelijking met (x, y).
   4. Dit is indrukwekkend: het gebruik en toepassen van gegevens in een rekenmachine. En, als je leraar krijgt, kun je er een vergelijking van een lijn met behulp van de lineaire regressie van de data die is net zoiets als een gemiddelde automatisch gedaan door een rekenmachine met ingebouwde programma's en automatisch grafieken te vinden. Wow! Dat moet een lange tijd te komen nadat je leren om het allemaal te doen met de hand. De calculator is een hulpmiddel om te gebruiken als je eenmaal bent of moet een goede technicus van algebra.
      

   • Het cartesiaanse coördinatenstelsel dat wordt gebruikt in de algebra voor grafische vergelijkingen, enz. werd vernoemd naar de Franse uitvinder van het gebruik van coördinaten op kaarten De Carte. Vergelijkbare mapping systemen worden gebruikt in alle soorten wiskunde, astronomie, navigatie, het aansteken van de pixels op computerschermen, verlichting bollen op borden en op scoreborden-echt, te plaatsen of te lokaliseren vrijwel alles.
   • Probeer uw antwoorden in problemen te controleren. Als u hebt of het oplossen van de x-en y-coördinaten, steek ze terug in de vergelijking. Bijvoorbeeld, als x = 10, dat wil zeggen: x bleek te zijn 10, in de vergelijking y = x 3, en sluit vervolgens tien voor x. Het antwoord moet de bijbehorende y-coördinaat, y = 13.
     • y = x 3 betekent y = 1x + 3, zodat de m = 1 is de helling, dat wil zeggen: de snelheid van verandering is 1, en dus m = dx / dy is 1/1 - die we kunnen gebruiken om betekenen: dat indien zowel het verschil in d x en d verschil in y verandering in hetzelfde tempo, en dan, als bijvoorbeeld helling m is gebaseerd op (8 en 8 over) op een coördinaat grafiek, dat zou betekenen dat m = (8/8) en dus m = 1 als 8/8 wordt vereenvoudigd tot de laagste termen. y = (8/8) x +3 is gelijk aan y = 1x 3 en eenvoudig y = x +3 (omdat ze allemaal vertegenwoordigen en grafiek als dezelfde lineaire uitdrukking, namelijk: ze beschrijven dezelfde lijn).

   Waarschuwingen en wat hulp

   • Vergeet niet om zich te vermenigvuldigen voor het toevoegen bij het ​​gebruik van y = mx + b, dus, niet toe x + b, maar eerst vermenigvuldig m. keer x.
     • Als je 25 (20) + 60 in de rekenmachine, zal het automatisch vermenigvuldigen 25 keer 20 eerste, dus maak je geen zorgen over te maken.
     • 25 (20) + de constante, b, en dus hebben we = _______ + 60 = _______? We weten dat de y-as b = 60 is de eerste (begin) punt. (Je zou kunnen noemen b = 60 de "kogelgat" waar de lijn y = 25x + 60 hits en schiet door de y-as -. Alsof de lijn is een lineair pad van een kogel Als je het pad van kunnen plotten kogel, als een lijn...).
   • Let op: voor het vinden van 25 (20) + 60 met de hand, als je probeert eerst 25 (20 +60) toe te voegen = 25 (80) = _______, dan is dat verkeerd! Dat is niet wat de regel a = mw + c (dat geeft ons y = 25x + 60) middelen. Je moet PEMDAS gebruiken Dus vermenigvuldigen komt voor het toevoegen en / of af te trekken.
     • Opmerking: Hoe pemdas gebruiken betekent gebruik / werken met deze "P een rentheses (groeperen van symbolen), E Pa> xponents, M ultiply EN OF D Vermenigvuldig> ivide, dan is A dd EN OF S Toevoegen> ubtract" in die volgorde, algemeen spreken of noodzakelijk voor degenen die aanwezig waren in de expressie / probleem om de volgorde van bewerkingen toepassing nodig zijn. PEMDAS maakt geen melding van "radicalen" zoals de vierkantswortel, maar dat wordt gebruikt, zoals haakjes, of andere groepering symbolen.
     • Opmerking: De "mnemonic-woord '(geheugenapparaat)" PEMDAS "drukt de order voor de vereenvoudiging of de evaluatie van de gebruikelijke wiskundige verklaring (als verschillende gegroepeerde en niet-gegroepeerde elementen zijn te vinden in een probleem). Weet jij dat? Nou, dat is niet het belangrijkste deel van dit artikel, maar je echt nodig hebt om te leren over het ooit tot algebra beter te begrijpen.
     • Opmerking: Ook de omgekeerde volgorde is nuttig vereenvoudigen en oplossen voor x in vergelijkingen met een onbekende x, de onbekende wordt gevonden door rekening en met "SAMDEP" of SAMDEP vrijwel zo in die volgorde op beide zijden van de vergelijking ( als en wanneer ze worden elk gevonden in de expressie / probleem) te vereenvoudigen, of oplossen.
   • Nooit stoppen met het beoefenen van uw Algebra, Biologie, Scheikunde en Meetkunde, etc. totdat je het begrijpt achteren en naar voren. Praktijk door het gebruik van applicaties (story problemen) die zijn een geweldige manier die je kunt krijgen en houden uw inzichten en vaardigheden vers!