Hoe het oppervlak van prisma voorbeeld

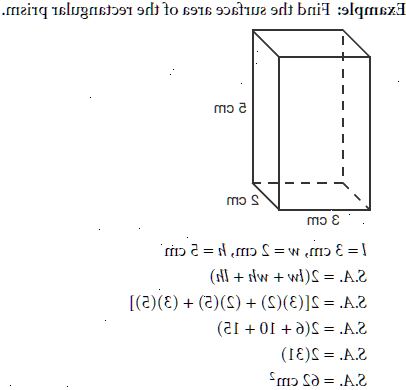
1. 1
   Label zoveel kanten als je kunt. Het leuke van prisma's is dat het overeenkomende einde paren maken het eenvoudig om een ​​groot deel van de individuele metingen te bepalen zonder te hoeven lossen voor iets. Elke meting die wordt gegeven voor een van de eindvormen (bijv. hoogte van de driehoek, straal van de cirkel) ook voor de overeenkomstige vorm aan de andere kant. Bovendien, als je weet dat de lengte van een zijde van het prisma, weet je de lengte van alle kanten. Verdeel deze nummers als nodig is om uw prisma om te zien wat je hebt om mee te werken.

Bereken de oppervlakte van een van de uiteinden bijpassende

1. 1
   Als er teveel uiteinden driehoeken, vindt het gebied van een driehoek gebruikt.
2. 2
   Als de bijpassende uiteinden zijn vierkant of rechthoekig, vermenigvuldig basis door de hoogte. De basis en hoogte zijn eenvoudig de afmetingen van twee loodrechte zijden van het vierkant of een rechthoek, een vierkant, deze twee afmetingen gelijk. Vermenigvuldigt beide getallen samen het gebied van het einde voorbeeld.
3. 3
   Als er teveel uiteinden cirkels, vermenigvuldigen pi door de straal kwadraat. De straal is de lengte vanaf het midden van de cirkel naar de buitenrand. Kwadratuur van dit aantal (dwz vermenigvuldig het met zichzelf) en het resultaat te vermenigvuldigen met pi (3.14159...). Dit geeft u de ruimte van het einde.
   • Als je hebt gekregen van de diameter (dwz de lengte over de gehele cirkel), verdeel dit aantal in de helft van de straal te vinden.
   • Als je hebt gekregen van de omtrek (dwz de lengte van de buitenste rand van de cirkel), deel dit getal door pi en verdeel dat resultaat met 2 om de straal te vinden.
4. 4
   Als de bijpassende uiteinden zijn parallellogrammen, vermenigvuldig basis door de hoogte. Parallellogrammen zijn schuin vierkantjes (zoals open dozen die opzij geduwd), ze hebben twee paar evenwijdige zijden maar geen van de hoeken rechte hoeken. De basis van een parallellogram is gewoon de lengte van een van de twee lange zijden uitgelijnd, de hoogte, echter de afstand tussen deze twee kanten, niet de lengte van een van de schuine zijden. Indien deze hoogte nog niet is gegeven aan u, het probleem zal u vragen op te lossen voor het door het inschakelen van de schuine kanten in een rechthoekige driehoek en geven u de lengte van twee van de zijden van de driehoek. Voor het oplossen van de hoogte op deze manier:
   • Gebruik de Stelling van Pythagoras, dat is A ^ 2 + b ^ 2 = c ^ 2. De hypotenusa van de driehoek of C, is gewoon de zijde van de driehoek tegenover de rechte hoek. We zullen de andere zijde die is gegeven roepen B C,>. Voor het oplossen van de hoogte, die we zullen noemen A, herschikken de formule naar A ^ 2 = C ^ 2 - B ^ 2. Vermenigvuldig C op zichzelf, dan vermenigvuldig B vanzelf. Trek de tweede resultaat van de eerste om zich te A ^ 2; om vervolgens op te lossen voor A, vinden de vierkantswortel van dit bedrag. Dit is de hoogte van het parallellogram, dat je nu vermenigvuldigen met de basis van het totale gebied.
5. 5
   Als de bijpassende uiteinden zijn een andere veelhoek, breken de vorm naar beneden in driehoeken op te lossen. Een vijfhoek, bijvoorbeeld, kunnen worden onderverdeeld in 5 gelijke driehoeken, een zeshoek kan worden opgesplitst in 6, en ga zo maar door. Wanneer u klaar bent met het tekenen van de driehoeken, op te lossen voor de oppervlakte van een driehoek gebruikt. Als je klaar bent, vermenigvuldig dat gebied door het totale aantal gelijke driehoeken die je hebt getekend.
   • Als de polygoon niet kan worden opgesplitst in perfecte driehoeken, breken in driehoeken en vierkanten. Bereken de oppervlakte van elke vorm afzonderlijk met behulp van de vorm gidsen hierboven en voeg ze samen om de totale oppervlakte van de polygoon te vinden.
6. 6
   Let op het gebied van de daartoe op uw papier en laat het met rust. Je zult het later terug te komen.

Vind de omtrek van een van de uiteinden bijpassende

1. 1
   Lossen voor eventuele ontbrekende kanten. Na het oplossen van gebied, kan je al de lengte van elke zijde van de vorm te kennen aan het einde van uw prisma. Zo niet, oplossen via een van de volgende methoden:
   • Als de bijpassende uiteinden zijn driehoeken, lossen voor alle partijen met behulp van de stelling van Pythagoras. De stelling van Pythagoras is A ^ 2 + b ^ 2 = c ^ 2: A en B zijn de basis en de hoogte van een rechthoekige driehoek en C is de schuine zijde, dat is gewoon de zijde tegenover de rechte hoek.
     • Als je hebt gekregen A en B, gebruikt u de formule C ^ 2 = A ^ 2 + B ^ 2. Vermenigvuldig Een op zichzelf, vermenigvuldig B op zichzelf, en samen voeg de twee nummers, dit geeft je C ^ 2. Om vervolgens op te lossen voor C, gewoon vinden de vierkantswortel van dit bedrag.
     • Als je hebt gekregen C en B: gebruik de formule A ^ 2 = C ^ 2 - B ^ 2. Vermenigvuldig C op zichzelf, vermenigvuldig B op zichzelf, en trek het tweede resultaat van de eerste, dit geeft je A ^ 2. Om vervolgens op te lossen voor A, gewoon vinden de vierkantswortel van dit bedrag.
     • Als je hebt gekregen C en A: gebruik de formule B ^ 2 = C ^ 2 - A ^ 2. Vermenigvuldig C op zichzelf, vermenigvuldig Een op zichzelf, en trek het tweede resultaat van de eerste, dit geeft je B ^ 2. Om vervolgens op te lossen voor B, gewoon vinden de vierkantswortel van dit bedrag.
   • Als de bijpassende uiteinden zijn cirkels, vinden de omtrek. De formule voor de omtrek is C = D x pi: C is de omtrek en D is diameter. Als je de straal, gewoon vermenigvuldigen met 2 om de diameter te vinden.
   • Als de bijpassende uiteinden zijn een andere veelhoek, breken de vorm naar beneden in driehoeken en / of pleinen als voorheen en vind de buitenranden door het oplossen van deze vormen afzonderlijk. Gebruik de vorm gidsen bovenstaande indien nodig.
2. 2
   Markeer de omtrek metingen op uw papier. U kunt ze gebruiken om het gebied van de zijden van het parallellogram bepalen.

Vind het oppervlak aan elke zijde

1. 1
   Let op de lengte van het prisma. Dit is de afstand tussen de twee bij elkaar horende uiteinden van de prisma. Aangezien de einden van het prisma parallel, zal deze afstand uniform zijn overal - zelfs als de overeenkomende beide uiteinden gebogen. Dit betekent dat als je weet dat de lengte van een kant, weet je de lengte van alle kanten.
2. 2
   Vind het oppervlak aan elke zijde. Elke zijde zal ofwel een vierkant / rechthoek of een parallellogram. Parallellogrammen zijn schuin vierkantjes (zoals open dozen die opzij geduwd), ze hebben twee paar evenwijdige zijden maar geen van de hoeken rechte hoeken.
   • Om de oppervlakte van een vierkant / rechthoek vinden, vermenigvuldig basis door de hoogte. De basis en hoogte zijn eenvoudig de afmetingen van twee loodrechte zijden van het vierkant of een rechthoek, een vierkant, deze twee afmetingen gelijk. Vermenigvuldigt beide getallen samen het gebied van het einde voorbeeld.
   • Om de oppervlakte van een parallellogram vinden, vermenigvuldig basis door de hoogte. Merk op dat de basis van een parallellogram is gewoon de lengte van een van de twee lange zijden uitgelijnd, de hoogte, echter de afstand tussen deze twee kanten, niet de lengte van een van de schuine zijden. Als je alleen weet dat de lengte van de schuine kant, maar niet het parallellogram de ware hoogte, trek een lijn door beide zijden van het parallellogram, veranderen in een perfect vierkant / rechthoek met een driehoek op beide zijden. Om de hoogte met behulp van deze driehoek te vinden:
     • Gebruik de Stelling van Pythagoras, dat is A ^ 2 + b ^ 2 = c ^ 2. De hypotenusa van de driehoek of C, is gewoon de zijde van de driehoek tegenover de rechte hoek. We zullen de andere zijde die is gegeven roepen B C,>. Voor het oplossen van de hoogte, die we zullen noemen A, herschikken de formule naar A ^ 2 = C ^ 2 - B ^ 2. Vermenigvuldig C op zichzelf, dan vermenigvuldig B vanzelf. Trek de tweede resultaat van de eerste om zich te A ^ 2; om vervolgens op te lossen voor A, vinden de vierkantswortel van dit bedrag. Dit is de hoogte van het parallellogram, dat je nu vermenigvuldigen met de basis van het totale gebied.
   • Als het prisma cilindrisch voorbeeld het gebied van de zijden van omtrek, die je opgelost in de vorige paragraaf, de totale hoogte vermenigvuldigen. (Afbeelding heeft de cilinder een stuk papier gewikkeld, die een perfect vierkant of rechthoek wanneer uitgepakt, vormt. De omtrek kan dan worden gezien als de lengte van dat stuk stuk papier, die kunnen worden opgelost als elke vierkante door vermenigvuldigen lengte maal hoogte.)

Zoek de totale oppervlakte

1. 1
   Vermenigvuldig het gebied van het einde van het prisma met 2. Zoek het nummer dat u afgewaardeerd wanneer u opgelost voor het gebied van een van de bijpassende uiteinden en verdubbel het om rekening te houden de andere kant.
2. 2
   Tel de delen van de zijden van het prisma. Als uw prisma heeft driehoekige uiteinden, wordt u optelling van drie kanten, als ze vijfhoekig, wordt u het toevoegen van vijf kanten, enz. Als het prisma is cilindrisch, hoeft u niet om iets toe te voegen als er maar een "kant ".
3. 3
   Voeg de totale oppervlakte van de uiteinden van de totale oppervlakte van de zijden. Dit geeft u het totale oppervlak van het prisma.