Hoe maak je een exponentiële functie gegeven een tarief en een initiële waarde schrijven

Met behulp van de koers als de basis

1. 1
   Beschouw een voorbeeld. Stel dat een bankrekening wordt gestart met een 750€ borg en de rente is 3% per jaar verergerd. Zoek een exponentiële vergelijking modelleren van deze functie.
2. 2
   Ken de basisvorm. De vorm voor exponentiële vergelijking is f (t) = P ₀ (1 + r) ^{t / h} waarbij P ₀ de initiële waarde, t de tijd variabel is, r de snelheid en h is het aantal te zorgen units van t overeenkomen met de koers.
3. 3
   Sluit de initiële waarde voor p en de kosten voor r. U heeft f (t) = 1000 (1.03) ^{t / h.}
4. 4
   Vinden h. Denk na over uw vergelijking. Elk jaar, het geld stijgt met 3%, dus elke 12 maanden het geld stijgt met 3%. Omdat je nodig hebt om t in maanden geven, moet u verdelen t door 12, dus h = 12. De vergelijking is f (t) = 1000 (1.03) ^T/12. Als de units zijn dezelfde voor de snelheid en de t stappen, h is altijd 1.

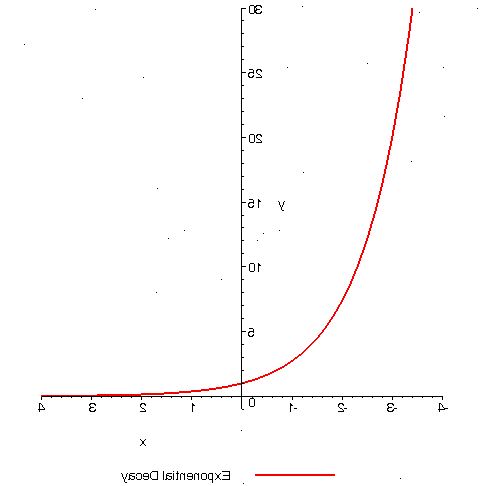
Met behulp van "e" als de basis

1. 1
   Begrijpen wat e is. Wanneer u de waarde e gebruiken als de basis, gebruikt u de "natuurlijke basis." Met behulp van de natuurlijke basis kunt u de continue groei rechtstreeks te trekken uit de vergelijking.
2. 2
   Beschouw een voorbeeld. Stel dat een 500 g monster van een isotoop van koolstof heeft een halfwaardetijd van 50 jaar (de halfwaardetijd is de tijd van het materiaal verzwakt zijn met 50%).
3. 3
   Ken de basisvorm. De vorm voor exponentiële vergelijking is f (t) = ae ^kt waarbij a de beginwaarde, e is de basis, k de constante groei, en t de tijd variabele.
4. 4
   Sluit de beginwaarde. De enige waarde die je krijgt die je nodig hebt in de vergelijking is de initiële groei. Dus, plug hem in voor een tot en met f (t) = 500e ^kt krijgen
5. 5
   Vind de continue groei. De continue groei is hoe snel de grafiek verandert op een bepaald moment. Je weet dat er in 50 jaar, zal het monster verval tot 250 gram. Die kunnen worden beschouwd als een punt op de grafiek die u kunt aansluiten inch Dus t is 50. Koppel hem aan te krijgen f (50) = 500e ^50k. U weet ook dat f (50) = 250, dus vervangen 250 voor f (50) aan de linkerkant om de exponentiële vergelijking te verkrijgen 250 = 500e ^50k. Nu naar de vergelijking op te lossen, knipt u eerst beide kanten door 500 te krijgen: 1/2 = e ^50k. Vervolgens neemt u de natuurlijke logaritme van beide kanten te krijgen:.. Ln (1/2) = ln (e ^50k Gebruik de eigenschappen van logaritmen om de exponent te nemen uit het betoog van de natuurlijke log en deze vermenigvuldigen met de log Dit resulteert in ln (1/2) = 50k (ln (e)). Bedenk dat ln is hetzelfde als log _e en dat de eigenschappen van logaritmen zeggen dat als de basis en het argument van de logaritme zijn hetzelfde, de waarde is 1. Daarom ln (e) = 1. Dus de vergelijking vereenvoudigt tot ln (1/2) = 50k, en als je delen door 50, leer je dat k = (ln (1/2)) / 50. Gebruik je rekenmachine om vind de decimale benadering van k tot ongeveer zijn -. 0,01386 Merk op dat deze waarde is negatief Als de continue groei is negatief, je hebt exponentiële afname, als het positief, je hebt exponentiële groei..
6. 6
   Sluit de k-waarde. Uw vergelijking is 500e ^{- 0,01386 t.}