Resistieve circuits kunnen worden geanalyseerd door het combineren van netwerken van parallel en serie weerstanden in een equivalente weerstand, vervolgens met behulp van de wet van Ohm om de stroom of spanning over die equivalente weerstand vinden. Zodra dit bekend is, is het mogelijk om terug te werken en het gebruik van Ohm recht berekenen van de spanning en stroom over de weerstand in het netwerk.
De vergelijkingen nodig zijn om de analyses uit te voeren worden kort geïntroduceerd, samen met uitgewerkte voorbeelden. Referenties worden aangehaald of gelinkt, maar genoeg informatie wordt hier gepresenteerd aan de concepten toe te passen zonder dat elders verwijzen. De stap-voor-stap stijl wordt alleen gebruikt in gedeelten waar meer dan een stap.
Alle opzettelijke weerstanden wordt getoond als weerstanden (schematisch, een zig-zag lijn). Verbindingen weergegeven als de lijnen worden verondersteld nul weerstand (ten minste bij benadering ten opzichte van de weergegeven weerstanden).
Samengevat, zijn de basisstappen hieronder weergegeven.
Stappen
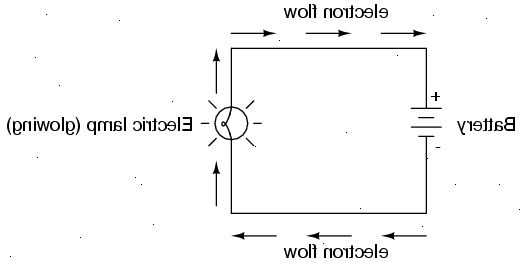
- 1Als er meer dan 1 weerstand in het circuit, vindt de equivalente weerstand "r" van het gehele netwerk zoals in "combinaties van weerstanden in serie en in parallel" hieronder.
- 2Gelden de wet van Ohm om deze waarde van "r" zoals wordt geïllustreerd onder "de Wet van Ohm" onderstaande.
- 3Als er meer dan 1 weerstand in het circuit, de waarde van spanning of stroom berekend in de voorgaande stap worden gebruikt in de wet van Ohm de spanning identificeert in of stroom via een andere weerstand in het netwerk.
De wet van Ohm
De wet van Ohm kunnen worden geschreven in 3 equivalente vormen afhankelijk van wat wordt opgelost:
(1) V = IR
(2) I = V / R
(3) R = V / I
"V" is de spanning over de weerstand (de "potentiaalverschil"), "I" is de stroom door de weerstand, en "R" is de waarde van de weerstand. Als de weerstand een weerstand (een component met een gekalibreerde waarde van de weerstand) wordt gewoonlijk aangeduid met "R" gevolgd door een getal, zoals "R1", "R105", etc.
Vorm (1) wordt gemakkelijk omgezet in vormen (2) of (3) door algebraïsche manipulaties. In sommige gevallen de letter "E" in plaats van "V" (bijvoorbeeld E = IR), waarbij "E" staat voor EMF of "elektromotorische" dat is een andere naam voor spanning.
Vorm (1) wordt gebruikt wanneer de stroom bekend is via een weerstand van bekende waarde.
Vorm (2) wordt gebruikt wanneer de spanning bekend is over een weerstand van bekende waarde.
Vorm (3) wordt gebruikt als de weerstand waarde niet bekend, maar de spanning over het en stroomvorm bekend, waardoor de weerstand berekend.
De standaard () eenheden van elke parameter in de wet van Ohm zijn:
- Spanningsval over de weerstand "V" is, afgekort "V". De afkorting "V" voor "volt" is niet te verwarren met de spanning "V" in de wet van Ohm.
- Voor deze "I" is in ampère, vaak afgekort tot "versterkers", afgekort "A".
- Weerstand "R" is in ohm, vaak vertegenwoordigd door de Griekse symbool hoofdstad omega (Ω). Letter "K" of "k" betekent een multiplier van 'duizend' ohms, "M" of "MEG" betekent een multiplier "miljoen" ohms. Vaak Ω symbool niet geschreven na een vermenigvuldiger, bijvoorbeeld een 10.000 Ω weerstand wordt gewoonlijk aangeduid als "10K" dan "10 k Ω".
De wet van Ohm is van toepassing op elke circuit met alleen resistieve elementen (zoals weerstand onderdelen, of de weerstand van dirigenten als draden of PC board lopers). Als er reactieve elementen (spoelen of condensatoren) is niet rechtstreeks van toepassing in de vorm hierboven (de bovenstaande vergelijking bevat slechts "R", die geen inductie of capaciteit niet omvatten) getoond. De wet van Ohm kan op resistieve circuits of de aangelegde spanning of stroom DC (gelijkstroom), AC (wisselstroom), of een willekeurig tijd-variërende signaal onderzocht op elk moment van de tijd. Als de stuurspanning en stroom sinusvormig AC (zoals van een 60 Hz huishoudelijk stopcontact), de eenheden van spanning en stroom zijn meestal volt of ampère .
Voor meer informatie over de wet van Ohm, met inbegrip van hoe het kan worden afgeleid en zijn geschiedenis, zie de Wikipedia wet van Ohm artikel.
Voorbeeld: spanningsval over een draad
Veronderstellen we willen de spanningsval vinden over een draad bij een stroom van 1 ampère stroomt er doorheen. De draad weerstand meet 0,5 Ω. Gebruik vorm (1) van de wet van Ohm boven vinden we de spanningsval over de draad:
V = IR V> = (1, A) (0,5 Ω) = 0,5 V (dat wil zeggen 1/2 volt)
Als de huidige 60 Hz elektrische huishoudelijke stroom van 1 ampère AC RMS was geweest, zou het resultaat hetzelfde, (0.5) zijn geweest, maar de eenheden zou zijn geweest "volt AC RMS".
Weerstanden in serie
De totale end-to-end weerstand van een reeks weerstanden aangesloten "serie" (zie figuur) is de som van alle weerstanden. Voor "n" resistors gemerkt R1, R2,..., Rn.
R totaal = R1 + R2 +... + Rn
Voorbeeld: weerstanden in serie
Stel dat er 3 weerstanden in serie:
R2 = 22 Ohm
De totale end-to-end weerstand:
R totaal = R1 + R2 + R3 = 10 + 22 + 0,5 = 32,5 Ω
Weerstanden in parallel
De totale weerstand over een reeks weerstanden parallel (zie afbeelding rechts) wordt gegeven door:
Gemeenschappelijke notatie betekenis "parallel met" is om twee parallelle slashes ("/ /") schrijven. Zo kan R1 parallel aan R2 worden aangeduid als "R1 / / R2 '. Merk op dat R1 / / R2 = R2 / / R1. Een set van 3 weerstanden R1, R2 en R3 alle gelijktijdig kunnen worden aangeduid als "R1 / / R2 / / R3".
Voorbeeld: weerstanden parallel
Voor 2 weerstanden in parallel, R1 = 10 Ω en R2 = 10 Ω (beide dezelfde waarde), hebben we:
Ook vermeld als "de geringste" betekent dat de totale weerstand altijd kleiner dan de weerstand van de minste weerstand in het circuit zijn.
Combinaties van weerstanden in serie en in parallel
Netwerken combinaties van serie en parallel weerstanden kunnen worden geanalyseerd door ze te combineren in een "equivalent" of "totale" verzet.
Stappen
- 1In het algemeen, een combinatie van alle parallelle weerstanden in gelijkwaardige parallelle weerstanden met "weerstanden parallel" hierboven. Merk op dat als er parallelle takken die ook bevatten reeks elementen, die zich eerst worden gecombineerd door het toevoegen van de weerstanden in die tak.
- 2Combineer serieweerstanden door ze toe te voegen, om de totale weerstand van het netwerk te verkrijgen, r totaal.
- 3Gebruik de wet van Ohm om de totale stroom in het netwerk voor een bepaalde aangelegde spanning, of de totale spanning over het netwerk voor een bepaalde toegepaste stroom te vinden.
- 4De totale spanning of stroom berekend in de voorafgaande stap wordt gebruikt om spanningen en stromen berekenen in het netwerk met de wet van Ohm.
- 5Breng deze stroom of spanning aan de wet van Ohm de spanning identificeert in of stroom via een andere weerstand in het netwerk. Dit wordt het kort tonen het voorbeeld hieronder.
Merk op dat de eerste 2 stappen hierboven moet mogelijk iteratief worden toegepast voor grote netwerken.
Voorbeeld: serie / parallel netwerk
Rechts voor het netwerk blijkt enerzijds de parallelle weerstanden worden gecombineerd met R1 / / R2, dan is de totale weerstand van het netwerk (over de aansluitingen) wordt gevonden van voorbeeld:
R totaal = r3 + R1 / / R2
Stel dat R3 = 2 Ω, R2 = 10 Ω, R1 = 15 Ω, en een 12 V accu wordt aangebracht over het netwerk, zodat V totaal = 12 volt. Oplossen met behulp van de bovenstaande stappen die we hebben:
De spanning over R3 (aangeduid VR3) kan nu worden berekend uit de wet van Ohm, aangezien de stroom door is bekend dat 1,5 ampère:
R3 = V (I totaal) (R3) = 1,5 x A 2 Ω = 3 volt
De spanning over R2 (die dezelfde als de spanning over R1) worden berekend met de wet van Ohm de stroom I = 1,5 ampère maal de equivalente parallel weerstand R1 / / R2 = 6 Ω vermenigvuldigen, waardoor 1,5 x 6 = 9 volt, of kan worden berekend door de spanning over R3 (V R3, net boven berekend) van de aangelegde spanning van 12 volt, dat is, 12 volt - 3 volt = 9 volt. Zodra dit bekend is de stroom door R2 (aangeduid I R2) kan worden berekend op basis van de wet van Ohm (waar de spanning over R2 wordt aangeduid met "V R2"):
R2 = I (V R2) / R2 = (9 volt) / (10 Ω) = 0,9 amp
De stroom door R1 kunnen eveneens worden gevonden met behulp van de wet van Ohm door het spanning over het (9 volt) door de weerstand (15 Ω), waardoor 0,6 ampère door R1. Merk op dat de stroom door R2 (0,9 ampère) plus de stroom door R1 (0,6 ampère) is gelijk aan de totale stroom in de terminals van 1,5 ampère.
