Geometrisch gemiddelde is een wiskundige concept dat gerelateerd is aan, maar gemakkelijk te verwarren met de meer algemeen gebruikte rekenkundig gemiddelde. Om het meetkundig gemiddelde berekenen, gebruikt u een van de volgende methoden.
Stappen
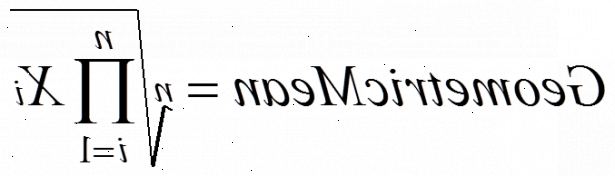
Twee nummers: eenvoudige methode
- 1Zoek de nummers die u wilt gemiddelde.
- Ex. 2 en 32.
- 2Vermenigvuldigen ze samen.
- Ex. 2 x 32 = 64.
- 3Bereken de vierkantswortel van het genoemde nummer.
- Ex. √ 64 = 8.
Twee nummers: gedetailleerde methode
- 1Steek uw nummers in de onderstaande vergelijking.
Als uw nummers 10 en 15, bijvoorbeeld, plug in 10 voor "eerste # 'en 15 voor' tweede #." - 2Lossen voor X.
Begin met cross-vermenigvuldigende waardoor de getallenparen diagonale elkaar vermenigvuldigen en vervolgens het instellen van de resultaten aan weerszijden van een = teken. Sinds X * X is X ^ 2, uw vergelijking eruit moet zien: X ^ 2 = (product van uw andere nummers).
Te lossen voor X, vinden de vierkantswortel van uw product. Als je geluk hebt, zal het resultaat een geheel getal te zijn. Zo niet, dan kunt u een decimaal antwoord geven of laat je antwoord in vierkantswortel vorm, afhankelijk van wat je instructeur geeft de voorkeur. Het voorbeeld hieronder is in vereenvoudigde vierkantswortel vorm.
Drie of meer nummers: eenvoudige methode
- 1Steek uw nummers in de onderstaande vergelijking.
Gemiddelde = (a 1 x een 2... a n) 1 / n- a 1 is een eerste getal, een 2 is een tweede getal, enzovoort
- n is het aantal inschrijvingen
- 2Vermenigvuldig de getallen (a 1, a 2, enz.) Samen.
- 3Bereken de n-de wortel van dit nummer. Dit is de geometrisch gemiddelde.
Drie of meer nummers: gedetailleerde methode
- 1Vind het logboek van elk nummer en samen voeg de logaritmische waarden.
Vind de LOG-knop op je rekenmachine. Als je klaar bent, type: (eerste nummer) LOG + (tweede nummer) LOG + (derde getal) LOG [+ log van extra nummers als nodig] =. Vergeet niet om te typen = Of het nummer dat u ziet zal het logboek van het meest recente nummer, niet het totaal te zijn.- Ex. log 7 + log 9 + log 12 = 2,878521796...
- 2Verdeel de som van de logaritmische waarden door het aantal waarden die u hebt toegevoegd. Als je de logs van drie nummers toegevoegd, te delen door drie.
- Ex. 2,878521796 / 3 = 0,959507265...
- 3Vind de antilog van uw resultaat. Op uw rekenmachine, drukt u op de 2e functie (meestal geel) en vervolgens LOG 2> om de secundaire functie van de log-knop, of de antilog activeren. Deze resulterende waarde is de geometrisch gemiddelde.
- Ex. antilog 0,959507265 = 9,109766916. Daarom is het geometrische gemiddelde van 7, 9 en 12 is 9.12.
Tips
- Verschil tussen de rekenkundige en meetkundige gemiddelde:
- Als je wilde het rekenkundig gemiddelde van 3, 4 en 18, bijvoorbeeld, zou je voeg 3 + 4 + 18, dan delen door 3, want er zijn drie nummers. Het resultaat zou 25/3 of ongeveer 8,333..., waaruit blijkt dat als je drie waarden van 8,3333..., zou het dezelfde totale als de individuele waarden van 3, 4 en 18 geven. Het rekenkundig gemiddelde antwoord op de vraag, "Als alle hoeveelheden dezelfde waarde had, wat zou die waarde moeten zijn om toe te voegen aan dezelfde totale?"
- Daarentegen is de geometrisch gemiddelde antwoord op de vraag "Als alle hoeveelheden dezelfde waarde, wat zou die waarde moeten zijn om hetzelfde product vermenigvuldigd? ' Dus om het geometrische gemiddelde van 3, 4 en 18 vinden, zouden we vermenigvuldigen 3 x 4 x 18. Dit zou ons 216. We zouden dan nemen de kubieke wortel (kubieke wortel want er waren drie originele nummers). Het antwoord zou zijn 6. Met andere woorden, omdat 6 x 6 x 6 = 3 x 4 x 18, 6 is het geometrische gemiddelde van 3, 4 en 18.
- Het geometrisch gemiddelde van een reeks getallen altijd kleiner dan of gelijk aan het rekenkundig gemiddelde van die set. Zie wikipedia: AM-GM_inequality
- De geometrisch gemiddelde geldt alleen voor niet-negatieve getallen. In woord problemen waar het gebruik van een geometrisch gemiddelde geschikt is, het scenario zal meestal geen zin met negatieve getallen.
