Visualiseren twee punten, A en B, verbonden door een rechte lijn. Stel je nu voor het tekenen van een tweede lijn precies door het midden van de eerste, op precies 90 graden aan de eerste. Deze tweede lijn is een middelloodlijn.
Meetkundig gesproken, een middelloodlijn is een groep punten (technisch een "locus") die op gelijke afstand van zowel A en B. De vorm van de groep vormt altijd een lijn. Elk punt op de middelloodlijn is zo ver van punt A vanaf punt B. In dit artikel wordt beschreven hoe u de vergelijking van de middelloodlijn vinden, ervan uitgaande dat u de coördinaten van de punten A en B.
Stappen
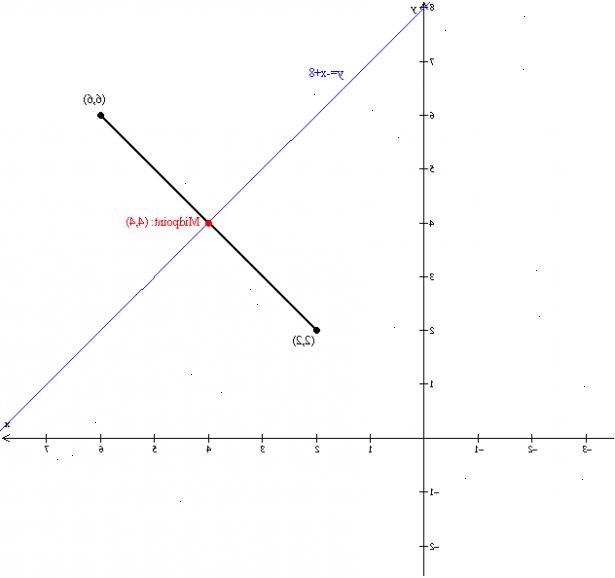
- 1Zoek de helling tussen de twee punten. Voor informatie over hoe dat te doen, raadpleeg dan het artikel Hoe helling (in de algebra) begrijpen.
- 2Neem die helling en vind de negatieve wederkerigheid. Met andere woorden, flip de fractie over, en verander het teken.
- Bijvoorbeeld: als je begint met 4/9, de negatieve wederkerigheid is -9/4.
- Bijvoorbeeld: als je begint met 5, u het in een fractie door een 1 eronder, zoals deze: 5/1. Vervolgens wordt de negatieve reciproke is -1 / 5.
- Bijvoorbeeld: als je begint met -7/3, de negatieve wederkerigheid is 3/7.
- Vergeet niet, als je begint met een negatieve fractie, zal de negatieve wederzijdse uiteindelijk positief!
- 3Vind het middelpunt van de twee punten. Het middelpunt ligt op de lijn van A naar B, halverwege tussen A en B.
- Voeg de x-coördinaat van A met de x-coördinaat van B, dan door twee gedeeld. Dit is de nieuwe x-coördinaat van het middelpunt.
- Voeg de y-coordinaat van een met de y-coördinaat van B, dan door twee gedeeld. Dit is de y-coördinaat van het middelpunt.
- 4Met behulp van dit middelpunt, en de negatieve wederzijdse uit stap 2, het berekenen van de vergelijking van de lijn. Voor meer informatie over hoe dit te doen, raadpleeg dan het artikel Hoe de vergelijking van een lijn te vinden.
