Een regelmatige veelhoek is een 2-dimensionale convexe figuur bestaande uit congruente zijden en hoeken gelijk in maat. Een convex figuur is een figuur met hoeken kleiner dan of gelijk aan 180 graden.
Dit artikel behandelt de wijze waarop aan de oppervlakte van regelmatige veelhoeken vinden met meer dan vier zijden. Als u wilt dat de oppervlakte van een vierhoek kennen, gaan. Als je wilt weten hoe je de oppervlakte van een driehoek te vinden, kunt u gaan
Stappen
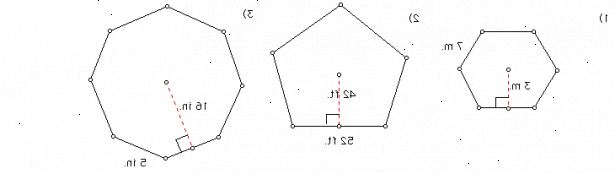
- 1Het gebied van een regelmatige veelhoek wordt gegeven door de formule:
Area = (AXP) / 2,
waarbij a de lengte van de apothem en p a> is de omtrek van de veelhoek.
Apothem het lijnsegment van het centrum van een regelmatige veelhoek aan het midden van een kant. Perimeter kan worden gevonden door de lengte zijde te vermenigvuldigen met het aantal zijden van de veelhoek. - 2Samen met de zijlengte, indien de lengte van de apothem ook rechtstreeks gegeven dan de vaststelling het gebied van dergelijke veelhoek is niet meer dan een taart lopen. Gewoon aansluiten op de waarden van a en p a> in de formule en krijgen de ruimte.
Denk bijvoorbeeld aan het vinden van de oppervlakte van een regelmatige zeshoek (6 zijden) van zijde lengte 10 eenheden en apothem meet 5sqrt (3) eenheden. - 3Samen met de zijlengte, indien de lengte van de apothem niet direct gegeven dan kan worden berekend met de volgende formule:
a = (s / 2) x kinderbed (180 0 / n),
waarbij a de lengte van de apothem, s a> is de zijlengte, en n het aantal zijden van de veelhoek.- Als voorbeeld, overweeg dan het vinden van de oppervlakte van een regelmatige nonagon (9 zijkanten) van zijde lengte 5 eenheden.
- Vind de apothem
- Vind de perimeter
- Vind het gebied met de in stap 1 hierboven genoemde formule.
- Als voorbeeld, overweeg dan het vinden van de oppervlakte van een regelmatige nonagon (9 zijkanten) van zijde lengte 5 eenheden.
Tips
- Voor meer informatie over het werken met wortels, kijk op de artikelen Hoe vierkantswortels vermenigvuldigen en Hoe vierkantswortels verdelen.
Waarschuwingen
- Als de tekening van uw achthoek (of wat dan ook) is gescheiden in driehoeken, en het gebied een driehoek wordt bestempeld, dan heb je niet nodig om de hele apothem zaken doen. Neem het gebied dat een driehoek, en vermenigvuldigen met het aantal zijden van de veelhoek oorspronkelijke.
