U waarschijnlijk al weet hoe om gebieden van rechthoeken en driehoeken te berekenen, maar hoe zit het ingewikkelder polygonen? Er is nog steeds een relatief eenvoudige methode om de berekeningen, mits jij de coördinaten van elk van de veelhoek.
Stappen
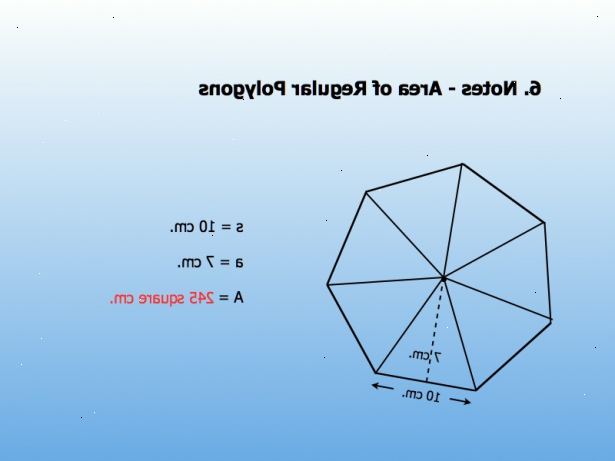
Regelmatige veelhoeken
- 1Om de oppervlakte van een regelmatige veelhoek vinden, lees dan hoe oppervlakte van regelmatige veelhoeken vinden
Onregelmatige veelhoeken
- 1Gebruik de coördinaten van de hoekpunten voor het vinden van de oppervlakte van onregelmatige veelhoeken. Het bepalen van het gebied voor een onregelmatige veelhoek kan worden gevonden wanneer je weet dat de coördinaten van de hoekpunten.
- 2Maak een array. Met de bovenstaande veelhoek als referentie, een lijst van de x en y coördinaten van elk hoekpunt van de veelhoek linksom volgorde. Herhaal de coördinaten van het eerste punt onder in de lijst, zoals:
- 3Vermenigvuldig de x-coördinaat van elk hoekpunt van de y-coördinaat van de volgende vertex. Voeg de resultaten.
- 4Vermenigvuldig de y-coördinaat van elk hoekpunt van de x-coördinaat van de volgende vertex en voeg deze resultaten.
- 5Trek de som van de producten berekend in stap 4 van de som van de producten van stap 3 zoals: (82) - (-38) = 120
- 6Het verschil wordt gedeeld door 2 tot de oppervlakte van de polygoon te krijgen: A = 120/2 = 60 vierkante eenheden.
Tips
- Als u een lijst van de punten in een klok mee in plaats van tegen de klok in, dan krijg je het negatieve van het gebied. Derhalve kan worden gebruikt als een instrument om de cyclische baan of sequentie van een bepaalde reeks punten die een veelhoek identificeren.
- Deze formule berekent met oriëntatie. Als je het gebruikt op een vorm waar twee van de lijnen kruisen als een cijfer acht, dan krijg je het gebied omringd linksom minus het gebied omringd met de klok mee.
