Hoe je twee stappen algebraïsche vergelijkingen op te lossen

Het oplossen van twee-staps vergelijkingen met slechts een variabele

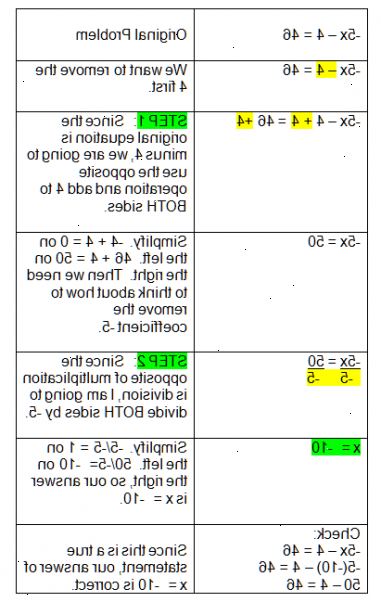
1. 1
   Dit proces is gemakkelijker als je een demonstratie volgen. We zullen het voorbeeld probleem gebruiken hier:-4x + 7 = 15
   
2. 2
   Verkrijg de variabele term zelf. De variabele term is de brief en wat coëfficiënt is aan de voorkant ervan. In ons geval hebben we de 4x-scheiden door uit de 7. Dit heet het Additive Inverse. We doen dit door het omkeren van de werking van de 7. In dit voorbeeld wordt het 7 wordt toegevoegd, dan moeten we aftrekken 7 van de linkerkant van de vergelijking. Om het evenwicht te houden, moeten we ook aftrekken 7 van de rechterkant:
   
   • Let op: wat je ook doet aan de ene kant van een vergelijking, moet je naar de andere kant Dit is de gouden regel van de Algebra.. Daarom 7 wordt afgetrokken van de 15 ook. We hoeven alleen aftrekken 7 keer per kant, dat is de reden waarom de 7 niet wordt afgetrokken van de-4x ook.
3. 3
   Omlaag brengen van de variabele looptijd. Herschrijf de vergelijking met de additieve inverse actie uitgevoerd. Onze nieuwe vergelijking is-4x = 8
   
4. 4
   Elimineer coëfficiënt van de variabele. "Coefficient" is het juiste woord voor het getal aan de variabele. In dit voorbeeld is de coëfficiënt -4. Net zoals we geëlimineerd de 7, dus zullen we elimineren de -4. Zoals het is te vermenigvuldigen met de x, keren we het vermenigvuldigen en delen aan iedere kant van -4. De formule hiervoor is -4 (x) ÷ -4 = 8 ÷ -4. -4.
   
   • Nogmaals, wat je ook doet om de vergelijking moet worden gedaan aan beide zijden. Daarom zie je twee keer ÷ -4.
5. 5
   Bereken het resultaat. -4x ÷ -4 = x, en 8 ÷ -4 = -2. Daarom x = -2
   
6. 6
   Label het antwoord, indien nodig. Als de vergelijking maakte deel uit van een verhaal probleem, bijvoorbeeld, zouden we willen het label
   

Additionele voorbeelden

1. 1
   Soms moet je het constant naar links in plaats van naar rechts:
   
   • In dit geval 11 = 3 - 7x. Trek 3 van beide kanten, dus onze vergelijking wordt:
     • 8 =-7x.
   • Annuleert de x door deze te delen door 7. Voer de bewerking aan beide zijden:
     • 8 ÷ -7 = x
     • -8/7 = X
     • -1.14 = X
   • Opmerking: u kunt ook de vergelijking omdraaien: 3 - 7x = 11 -> x = 1,14
2. 2
   Soms is de laatste stap is om in plaats van verdelen vermenigvuldigen:
   
   • Aangezien de vergelijking x / 5 + 7 = -3
   • Aftrekken 7 van beide kanten:
     • (X / 5 + 7) - 7 = -3 - 7, of x / 5 = -10
   • Sinds 5 is de noemer, vermenigvuldigen in plaats van verdelen elke kant door 5 om de 5 opheffen.
     • (X / 5) * 5 = -10 * 5 of x = -50

Oplossen van vergelijkingen met een variabele per kant

1. 1
   Controleer dat beide variabelen gebruiken dezelfde letter. Als ze dat niet doen, dan is deze methode niet zal werken.
   
2. 2
   Verplaats de constanten naar rechts door hun inverse. (Als het wordt toegevoegd, moet je aftrekken, en vice versa.
   
   • In deze voorbeeld-2x - 3 = 4x - 15. Annuleert de drie:
   • (-2x - 3) 3 = (4x - 15) 3 =-2x = 4x - 12
3. 3
   Verplaats de variabelen aan de linkerkant door het toevoegen van hun inversies:
   
   • -2x - 4x = (4x - 12) - 4x =-6x = -12
4. 4
   Verdeel de coëfficiënt, indien nodig.
   
   • -6x ÷ -6 = -12 ÷ -6
   • x = 2
5. 5
   Deze methode benadrukt eindigen met de variabele links. Dat is niet strikt noodzakelijk. Echter, als je net begint met het oplossen van vergelijkingen, het is de aanbevolen methode omdat het geen onafhankelijke besluitvorming vereisen.