Hoe je vectoren optellen of aftrekken

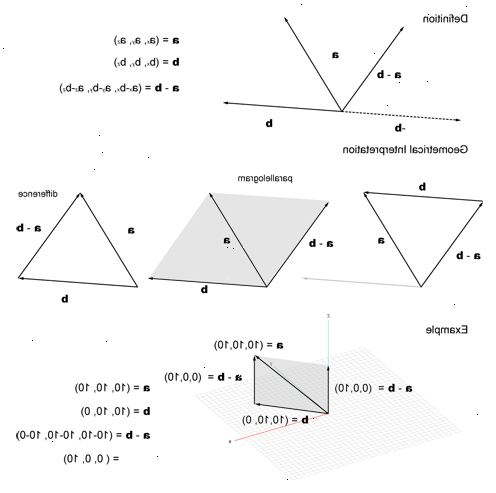
Vector optellen of aftrekken stappen

1. 1
   Als we 2 vectoren, vector A en vector b,
   • A = <a1,b1,c1>
   • B = <a2,b2,c2>
2. 2
   Als we willen vector A naar vector b, voeg dan
   • A + b = <a1+a2,b1+b2,c1+c2>
3. 3
   Als we willen vector aftrekken Een van vector b, dan
   • Ab = <a1-a2,b1-b2,c1-c2>

Methode een: kop tot staart

1. 1
   Neem een willekeurige vector, en identificeren van de kop en de staart. U kunt een tekening op schaal, of een ruwe schets te maken. Als u het maken van een tekening op schaal, moet u zorgen voor de bouw van alle kanten zeer zorgvuldig.
2. 2
   Schuif een andere vector, zodat zijn staart verbindt met het eerste het hoofd
3. 3
   Word lid van alle andere vectoren later. De volgorde maakt niet toe, en deze werkwijze kan worden gebruikt voor een aantal vectoren. Zij moeten echter worden gericht zodat ze beginnen een veelhoek vormen.
4. 4
   Doe mee aan de staart van de eerste vector naar de kop van de laatste. Dit is de resulterende vector, of de som van alle vectoren.
   • Als je het tekenen van het diagram om een ​​schaal, tekening precies alle hoeken, kunt u de lengte van de resulterende vector met behulp van een liniaal. Ook dan is, meet de hoek die de resulterende maakt met ofwel een gespecificeerde vector, of de horizontale / verticale etc.
   • Als je het maken van een schets, moet u de grootte van de resulterende met driehoeksmeting berekenen. U kunt hier het en het behulpzaam. Als u samen het toevoegen van meer dan twee vectoren, is het nuttig om de eerste twee toe te voegen, en gebruik vervolgens de resulterende met de derde vector, en ga zo maar door.
5. 5
   Vertegenwoordig uw resulterende vector. Bijvoorbeeld, als de vectoren weergegeven snelheden en toets "Een snelheid van x ^{ms-1 bij} y ^o de horizontale / verticale / etc".

Methode twee: loodrechte componenten

Deze methode wordt meestal gebruikt in de Cartesiaanse vlak, maar kan worden gebruikt voor andere vectoren ook.

1. 1
   Gesplitst elke vector in twee loodrechte componenten. Bijvoorbeeld, elke vector splitsen in zijn horizontale en verticale componenten. Het is gebruikelijk om vectoren splitsen in componenten langs de x-en y-assen in het platte vlak. De eenheidsvector langs de x-as wordt conventioneel geschreven als i, die langs de y-as als j.
   • Om een ​​kracht te lossen in componenten, moet u de hoek die het maakt met de horizontale, verticale, x-as of de y-as weten. Zodra deze hoek bekend is, kan een rechthoekige driehoek construeren met de kracht hypotenusa en de beide andere zijden langs de x-en y-assen. De lengten van de beide andere zijden zijn de grootten van de componenten in die richtingen, en kan worden berekend met behulp van driehoeksmeting. De zijkant naast de hoek x cos (hoek) en de andere zijde is x sin (hoek), waarbij x de grootte van de oorspronkelijke werking.
   • Indien de punten a component naar links of naar beneden, krijgt een minteken (-).
2. 2
   Voeg alle grootten van de horizontale componenten (of die langs de x-as) bij elkaar. Afzonderlijk, voeg alle grootten van de verticale componenten (of die langs de y-as). Als een component een minteken (-), wordt de magnitude afgetrokken, dan toegevoegd.
3. 3
   Bereken de grootte van de resulterende met de stelling van Pythagoras. De stelling kan worden vermeld: c ² = a ² + b ^2, c de grootte van de resulterende vector, a de grootte van de som van de componenten langs de x-as, en b is de grootte van de som van de componenten langs de y-as.
4. 4
   Bereken de hoek die de resulterende maakt met de horizontaal (of de x-as). Gebruik de formule θ = tan ^-1 (b / a), waarin θ de hoek is die de resulterende maakt met de x-as of de horizontale.
5. 5
   Vertegenwoordig uw resulterende vector.
   • Bijvoorbeeld, als de vectoren weergegeven krachten en voer "een kracht van x y ^o N op de horizontale / x-as / etc".

Methode drie: vector aftrekken

1. 1
   Trek door het toevoegen van een negatieve. Aftrekken van een vector van elkaar kunnen worden gezien als toevoeging zijn "negatieve".
2. 2
   Vind de negatieve van de vector. Dit is dezelfde orde van grootte als de oorspronkelijke vector, doch tegengesteld in richting. U kunt haar te vertegenwoordigen door het maken van de originele vector, maar het tekenen van de pijl andersom, zodat de staart wordt het hoofd en de hoofdsteun wordt de staart.
3. 3
   Volg een aanvulling bovenstaande methode, met behulp van de negatieve. Gebruik een van de twee hierboven beschreven methoden toevoeging aan de "negatieve" of de vector worden afgetrokken en de vector moest worden afgetrokken voegen.