Wkonl

Hoe kunt u uw salaris verdubbelen met behulp van een algebraïsche maas in de wet

Wie het ook was die zei dat je kon krijgen nummer te zeggen wat was volkomen gelijk. Wat hij niet zei, was echter hoe enorm therapeutisch het is om hen te zeggen wat je wilt. Dus, geniet van de bevredigende proces van "bewijzen" wiskundig dat je echt 149.260€ / jaar, hebben een 10.000 vierkante voet naar huis, en worden zo fit als een hoentje door de volgende stappen.

Stappen

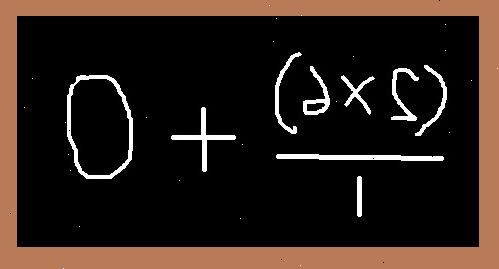
Hoe kunt u uw salaris verdubbelen met behulp van een algebraïsche maas in de wet. Schrijf 'gegeven a = b' op een nieuwe regel.
Hoe kunt u uw salaris verdubbelen met behulp van een algebraïsche maas in de wet. Schrijf 'gegeven a = b' op een nieuwe regel.
  1. 1
    Stroop je mouwen op. Dit volbrengt meer dan alleen het praktische voordeel van het niet krijgen van uw mouwen vuil en besmeurd met lood. Het laat toeschouwers weten dat je serieus bent over wiskundig bewijzen dat je echt een 6 '6 "persoon, alleen verstoord door het licht te laten uitzien als een 4' 3" persoon zijn. Ook, het is goed voor hen te laten weten dat je niets uit de mouwen hebben.
  2. 2
    Neem een vel papier en NB: Gebruik altijd een bij gebruik van algebraïsche achterpoortjes voor welk doel dan Sub-Note:.. Natuurlijk, zal je waarschijnlijk niet nodig om iets te wissen, maar dit zal blijken te zijn, want je gebruikt een; als je gebruik maken van een, zal je een fout maakt en zal wensen dat je gewoon had gebruikt een potlood in de eerste plaats.
  3. 3
    Schrijven aan de bovenkant van het papier het werkelijke aantal en de "echte" nummer. In het voorbeeld zal deze 3 ballen en 11 ballen zijn om aan te tonen dat de persoon die 3 bollen werkelijk 11.
  4. 4
    Schrijf 'gegeven a = b' op een nieuwe regel.
  5. 5
    Voer de volgende wiskundige bewerkingen:
    3a = 3b (Beide zijden door het getal te vermenigvuldigen)
    11a = 11b (Beide zijden van de "echte" nummer vermenigvuldigen)
    3a 2 = 3ab (Vermenigvuldigen met een aan beide zijden)
    11ab = 11b 2 (B vermenigvuldigen met aan beide zijden)
    3a 2 - 11ab = 3ab - 11b 2 (Aftrekken van de bovenstaande twee vergelijkingen een te maken)
    3a 2 - 3ab = 11ab - 11b 2 (Aftrekken 3ab en het toevoegen 11ab aan beide zijden)
    3a 2 - 3ab + ab - b 2 = 12ab - 12b 2 (Het toevoegen van ab en aftrekken b 2 van beide kanten)
    3a (ab) + b (ab) = 12b (ab) (Factoring out gemeenschappelijke factoren)
    3a + b = 12b (Het verwijderen van gemeenschappelijke factoren * Waarschuwing: deze stap deelt door 0, dat is algebraïsch ongedefinieerd en dus geldt niet in een proof)
    3a = 11b (B aftrekken van beide kanten)
    3b = 11b (Vervangen door een voor b, te beseffen dat ze gelijk zijn)
    3 = 11 (Het verwijderen van veelgebruikte termen)
  6. 6
    Teken een klein plein aan het einde van uw laatste regel en vul het in. Om een wiskundige, betekent "darn tootin" of "zaak gesloten" of "quod erat demonstrandum" of "deze logica is zo onweerlegbaar als de rattenvanger van pipe dit nadat zijn zoon liep over het met de grasmaaier "(nou ja, eigenlijk, dat laatste is" irreflutable, "maar het is waarschijnlijk passend hier toch).
  7. 7
    Geniet van de tevredenheid van, voor een ogenblik, met de zes-cijfer salaris en de ruime zomerhuis, verbazingwekkend genoeg, op de jonge leeftijd van 23! (Wow, je ziet er geweldig uit!) Of, natuurlijk, de tevredenheid van het zijn een meester jongleur, als dat is wat drijft uw boot.

Tips

  • Spoiler! niet lezen als je wilt uitzoeken voor jezelf waarom dit werkt niet echt Dit bewijs aast op een interessante wiskundige nee-nee, verborgen in de algebra van het bewijs: door nul. Merk op dat we in het begin dat besloten a = b. Dus, als we factor uit ab, zijn we eigenlijk allemaal termen van ab om dat te doen delen. Nou, ab is 0 omdat a en b gelijk zijn, en delen door 0 is illegaal. (Sneaky wiskundigen...) Hoe dan ook, er zijn veel variëteiten van deze mazen die, terwijl ze algebraïsch geluid lijken, zijn ze in werkelijkheid vals. Probeer het verbergen van de vierkantswortel van een negatief in een variabele of een denkbeeldig aantal. Welke andere dingen kunnen je 'bewijzen'?
  • Er zijn talloze nummers die mooier zou zijn als ze waren gewoon iets anders, leeftijd, GPA, credit card nummer, het bedrag dat u de creditcardmaatschappij te danken, en het aantal keren dat je te laat om deze week zijn geweest, gewoon om een paar.
  • Als je vooral nerdy voelt, probeer dan bewijst dat π = 3 of die e = 2. Nu, dat zou echt vereen-π leven!
  • Overweeg zorgvuldig de implicaties van het bewijs hierboven; zijn er geen problemen mee? Lees verder, als je wilt weten...