Wkonl

Hoe maak je een congruente driehoeken geometrie bewijs schrijven

Het schrijven van wiskundige bewijzen kan het moeilijkste deel van de geometrie, maar ze zijn essentieel. Elke geometrie boek heeft een sectie bewijzen, en congruent driehoek bewijzen nemen een groot deel. Aangezien het proces kan afhankelijk van je driehoeken en uw gegevenheden, je zelden volgt precies hetzelfde proces, dat kan erg frustrerend zijn. Maar er is een algemeen patroon, en het volgen van deze richtlijnen zal helpen.

Stappen

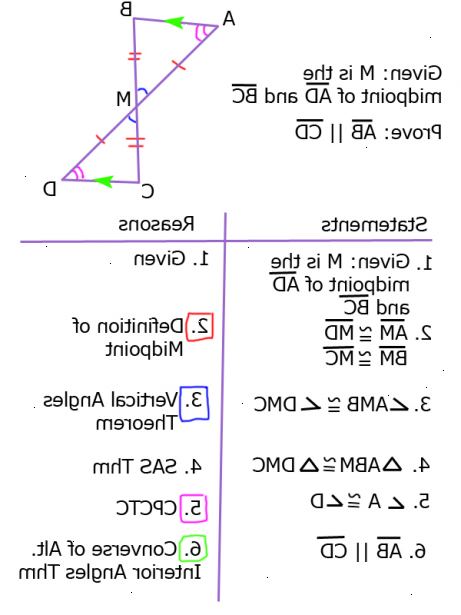
Hoe maak je een congruente driehoeken geometrie bewijs schrijven. Het opzetten van een twee-koloms proof-formaat.
Hoe maak je een congruente driehoeken geometrie bewijs schrijven. Het opzetten van een twee-koloms proof-formaat.
  1. 1
    Het opzetten van een twee-koloms proof-formaat. De de linkerkolom moeten worden geëtiketteerd "Statements" en de rechterkolom label "Reasons".
  2. 2
    Kopieer de afbeelding op het papier, vooral als de leraar vraagt ​​u om dit te doen.
  3. 3
    Lijst van uw gegevenheden als de eerste stap in uw verklaringen kolom. Onder de kolom redenen, moet je schrijft "gegeven".
  4. 4
    Vertaal de gegevenheden in nuttige informatie. Voor elk gegeven, wil je denken wat je zou kunnen doen met die kennis. Op dit punt in het bewijs, de meeste van uw redenen zal zijn definities.
    • Als het een van de gegevenheden is "Punt C is het middelpunt van AB ', zou uw verklaring te lezen" AC = CB "en de reden zou" Definitie van middelpunt "te zijn.
    • Als segment XY halveert segment NM, en P is het punt waar XY snijdt NM, zou uw verklaring te lezen "NP = PM 'en de reden zou" Definitie van bisector "te zijn.
    • Als de gegevenheden zeggen "KL staat loodrecht op HJ ', zou uw verklaring zijn" Angle KLH is een rechte hoek ". De letters is afhankelijk van het diagram, dat is een reden waarom het diagram belangrijk.
  5. 5
    Kijk voor alle gelijkbenige driehoeken in het diagram op basis van uw gegevenheden. Driehoeken gelijkbenige driehoeken zijn die twee benen van gelijke lengte hebben. Schrijf de twee benen zijn congruent als een verklaring onder vermelding "Definitie van gelijkbenige" als reden.
  6. 6
    Kijk voor parallelle lijnen. Indien een derde lijn loopt door hen beiden, zal het afwisselend interieur hoeken en bijbehorende hoeken vormen. Deze zijn heel gebruikelijk in driehoek bewijzen. De algemene vorm gevormd door de hoeken lijkt een de letter "z".
    • Schrijf in uw verklaringen column dat die hoeken zijn congruent aan elkaar met de reden hiervoor is "Alternate interieur hoeken zijn congruent" of "Overeenkomstige hoeken zijn congruent".
    • Gebruik geen redenen zoals "Definitie van parallelle" of "Definitie van alternatieve binnenhoeken". Dit zijn geen geldig bewijs redenen.
  7. 7
    Kijk in het schema voor de verticale hoeken. Verticale hoeken zal een X vormen en zijn de hoeken tegenover elkaar raken in het centrum, maar niet langs hun zijden. Deze verticale hoeken zijn congruent. Een voorbeeld zou zijn om de uitspraak "Angle P is congruent aan hoek R" gebruiken met de reden "verticale hoeken zijn congruent".
  8. 8
    Kijk in het schema voor eventuele lijnen of hoeken gedeeld door driehoeken. Dit is waar de reflexieve pand in het spel komt.
    • Uw verklaring moeten lezen "XY = XY" of "Hoek A = hoek A" en de reden zou zijn "Reflexive eigendom van congruentie".
  9. 9
    Overdragen elke congruentie verklaring die u tot nu toe hebt gevonden, waaronder de gegevenheden, in het diagram. Congruent kanten word gemarkeerd met hekjes; congruent hoeken zijn gemarkeerd met bogen.
  10. 10
    Kijken naar een van de driehoeken in de afbeelding. Opmerking alle markering die u zojuist gemaakt en degenen die werden gegeven aan u. Hoeveel hoeken congruent zijn? Hoeveel kanten? Match deze informatie met een van de driehoek congruentie stellingen. Uw verklaring moeten lezen "Driehoek ABC is congruent aan driehoek XYZ" en de reden zou de juiste keuze tussen AAS, ASA, SAS, SSS, HL, enz. worden
    • SSS staat voor kant, zijde, kant. Alle drie zijden moet zijn congruent.
    • Twee zijden en een hoek moeten congruent zijn om te kunnen worden SAS (zijde, hoek, side).
    • Kijk of je driehoeken congruent rechte hoeken, en twee congruente kanten, namelijk de schuine zijde (dat is de zijde direct tegenover de rechte hoek). Als ze dat doen, dan staat ze als congruent met de reden HL (Hypotenuse Been Stelling).
    • Het kan ASA AAS of als twee hoeken congruent, maar slechts een zijde.
  11. 11
    Kijk nog eens naar de "bewijzen" lijn van uw probleem. Als het is hetzelfde als uw laatste verklaring, dan bent u klaar.

Tips

  • Als uw diagram geen twee driehoeken, dan heb je misschien een ander soort bewijs hebben. Dubbel te controleren om ervoor te zorgen dat het probleem vraagt ​​om congruentie van twee driehoeken bewijzen.
  • Als uw diagram heeft twee overlappende driehoeken, probeer ze hertekenen als afzonderlijke driehoeken. Het zal veel eenvoudiger te vinden en markeer de congruente stukken.

Waarschuwingen

  • Als uw givens het woord "loodrecht," zeg niet dat een hoek van 90 graden te wijten aan de definitie van loodrechte lijnen. In plaats daarvan, schrijf een verklaring te zeggen zodanige hoek is een rechte hoek vanwege "definitie van loodrechte lijnen en schrijf dan nog een verklaring zeggen de genoemde hoek is 90 graden vanwege de" definitie van de rechte hoek ".
  • Je kunt niet bewijzen een stelling met zichzelf. Als je probeert te bewijzen dat basishoeken congruent zijn, zult u niet in staat zijn om te gebruiken "Base hoeken zijn congruent" als reden overal in uw bewijs.