Hoe maak je een vierkantswortel hand berekenen

Berekenen van een vierkantswortel hand

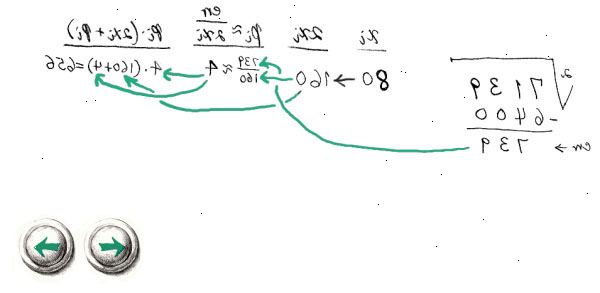
1. 1
   Noteer het nummer dat u wilt de vierkantswortel van berekenen. Scheid de cijfers in paren, uitgaande van de decimale punt: 79,520,789,182.47897 wordt "7 95 20 78 91 82 47 89 70.". Als een voorbeeld, probeer dan het berekenen van de vierkantswortel van 780,14. Trek twee lijnen als op de afbeelding en schrijf "7 80. 14 'aan de linkerkant. Op de top rechts, heb je de vierkantswortel van 780,14.
   
2. 2
   Kijk naar de meest linkse paar en vindt de grootste integer n die vierkant kleiner is dan of gelijk aan. Plaats n in het kwadrant rechtsboven, en berekent het kwadraat van n in de rechtsonder kwadrant. In het voorbeeld van dit artikel, dat paar is 7. En 2 x 2 ≤ 7 <3 x 3, dus n = 2. Schrijven 2 in het kwadrant rechtsboven: dat is het eerste cijfer van de wortel. Schrijf 2 × 2 = 4 in de onderste rechter kwadrant, je zal dat aantal in de volgende stap nodig.
   
3. 3
   Trek het nummer dat u net berekend vanaf de meest linkse paar. Bijvoorbeeld het artikel, aftrekken 4 van het paar "7", die geeft je 3.
   
4. 4
   Drop het volgende paar aan de linkerkant. Vermenigvuldig het aantal in het kwadrant rechtsboven door twee en schrijf het in de rechtsonder kwadrant, het toevoegen van "_ × _ =". In het voorbeeld, de volgende paar is "80": schrijf "80" naast de 3. Dan twee keer het aantal rechtsboven is 4: schrijf "4_ × _ =" in de rechter kwadrant.
   
5. 5
   Vind de grootste cijfer vervangen onderstreept zodat het resultaat van de vermenigvuldiging lager dan of gelijk aan het huidige aantal links. In het voorbeeld, als je vervangt de underscore met 8, 48 maal 8 is 384, die groter is dan 380. Dus 8 is te groot. Maar 7 zal werken. Schrijf 7 op het onderstreept, en bereken: 47 keer 7 gelijk aan 329. Schrijf 7 in de rechterbovenhoek: dat is het tweede cijfer van de vierkantswortel van 780,14.
   
6. 6
   Trek het nummer dat u net berekend op basis van het huidige nummer aan de linkerkant. In het voorbeeld aftrekken 329 van 380, wat 51 geeft.
   
7. 7
   Herhaal stap 4. Aangezien u bent nu ondervindt de decimale punt in 780,14, schrijf een decimale punt in de wortel, in de rechterbovenhoek. Laat de volgende paar (14) aan de linkerkant. Twee keer het nummer in de rechterbovenhoek (27) is 54, dus schrijf "54_ × _ =" in de rechter kwadrant.
   
8. 8
   Herhaal stap 5 en 6. Vind de grootste cijfer te vervangen de underscore en doe de vermenigvuldiging. In het voorbeeld, 549 keer 9 4941, die lager dan of gelijk aan het getal links (5114) is. Schrijf 9 in de rechterbovenhoek, en aftrekken van het resultaat van de vermenigvuldiging van het getal links: 5114 min 4941 is 173.
   
9. 9
   Als u wilt doorgaan met cijfers te berekenen, drop een paar nullen aan de linkerkant, en herhaal de stappen 4, 5 en 6.
   

Verklaren van het proces

1. 1
   Om te begrijpen hoe deze methode werkt, overweeg dan het nummer dat u het berekenen van de vierkantswortel van de oppervlakte S van een vierkant. Je proberen dan de lengte L van de kant van de vierkante berekenen. U wilt het nummer L vinden zodat L ² = S.
   
2. 2
   Neem aan dat je A het eerste cijfer van L (de vierkantswortel we proberen te berekenen) te bellen. B zal haar tweede cijfer, C zijn derde, enzovoort zijn.
   
3. 3
   Neem aan dat je sa de eerste paar cijfers van s, sb het tweede paar cijfers, etc noemen.
   
4. 4
   Net als in een divisie, waarin je alleen belangstelling voor de volgende een cijfer op een moment, hier in de calculus van de vierkantswortel, je geïnteresseerd bent door de volgende twee cijfers in een tijd (dat is de volgende een cijfer tijd voor de vierkantswortel). En ook, net als in een divisie, de positie van de decimale punt is niet belangrijk in het proces: je kunt altijd gewoon toevoegen aan het eind.
   
5. 5
   Kijk naar de eerste paar sa van cijfers van S (sa = 7 in het voorbeeld) en je wilt haar vierkantswortel vinden. Het eerste cijfer Een van die wortel is dan het grootste getal waar het plein niet meer dan Sa (wat betekent A zodat A ² ≤ Sa <(A 1) ²). In het voorbeeld S1 = 7 en 2 ² ≤ 7 <3 ², dus A = 2.
   
6. 6
   Merk op dat als je wilde verdelen 88.962 met 7, de eerste stap is vergelijkbaar zou zijn: je zou kunnen kijken naar het eerste cijfer van 88.962 (8) en je zou het grootste cijfer dat willen, wanneer vermenigvuldigd met 7, lager is dan of gelijk is 8. Wat betekent d zodat 7 × d ≤ 8 <7 × (d +1). d zou dan gelijk zijn aan 1.
   
7. 7
   Bereken het volgende cijfer B.
   
   • Overweeg (10A + B) ² = 100A ² + 2 × 10A × B + B ². (Anders 10A + B het aantal met B in de stand eenheden en A in de tientallen positie: met A = 1 en B = 2, 10A + B is eenvoudig het nummer 12.)
     (10A + B) ² is het gebied van de hele vierkant, 100a ² (10A + B) ²> het gebied van de grootste vierkant binnen, B ² de oppervlakte van de kleinste vierkant en 10a × b B ²> de oppervlakte van elk van de twee rechthoeken.
8. 8
   In stap 3, je een ² van sa aftrekken. Om rekening te houden met de factor 100, zet je een paar (Sb) van de cijfers van S: je wilt "Sa Sb" om de totale oppervlakte van het plein te zijn, en je afgetrokken 100A ² (de oppervlakte van het grote plein) van het. Wat overblijft is het aantal N1 verkregen links in stap 4 (380 in het voorbeeld). En dat aantal is gelijk aan 2 × 10A × B + B ² (oppervlakte van de twee rechthoeken plus oppervlakte van het kleine plein).
   
9. 9
   Kijk voor n1 = 2 × 10 a × b + b ², ook geschreven als n1 = (2 × 10 a + B) × B. Je weet N1 (= 380) en A (= 2), en je op zoek bent naar B. In de vergelijking, is het meest waarschijnlijk B niet van plan om een ​​geheel getal zijn, dus je moet eigenlijk vinden de grootste integer B zodat (2 × 10A + B) × B ≤ N1. (En B 1 te groot zou zijn, dus je hebt:. N1 <(2 × 10A + (B 1)) × (B 1))
   
10. 10
    Voor het oplossen van dat, vermenigvuldig A met 2, verschuiven in de positie van de tientallen (wat gelijk is aan vermenigvuldigen met 10), plaats B in de positie van de eenheden, en vermenigvuldig dat getal met B. Dat aantal is (2 × 10A + B) × B, en dit is precies wat je doet als je schrijft "N_ × _ =" (met N = 2 × A) op de onderste rechter kwadrant in stap 4. En in stap 5, vind je het grootste gehele getal B dat past op de underscore, zodat (2 × 10A + B) × B ≤ N1.
    
11. 11
    Trek het gebied (2 × 10 a + B) × B van het totale gebied (aan de linkerkant, zoals in stap 6), waarmee u de omgeving geeft s-(10a + b) ² nog niet verantwoord (en die zal worden gebruikt de volgende cijfers op soortgelijke wijze) te berekenen.
    
12. 12
    Naar het volgende cijfer c berekenen, herhaal het proces: drop de volgende paar (Sc) van S tot N2 te verkrijgen aan de linkerkant, en zoek naar de grootste C dus je hebt (2 × 10 × (10A + B) + C) × C ≤ N2 (gelijk aan het schrijven van twee maal het getal van twee cijfers "AB", gevolgd door "_ × _ =" en zoek naar de grootste cijfer dat past op de underscore).