Hoe je wiskundige waarschijnlijkheden vinden

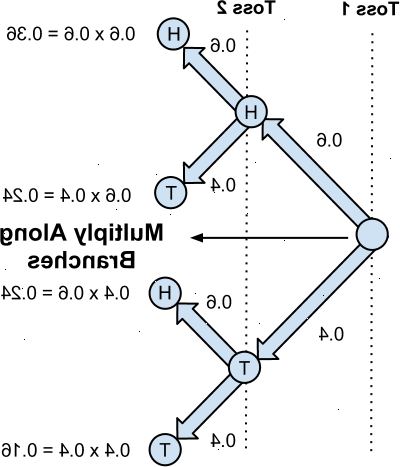
Waarschijnlijkheid van een onafhankelijke gebeurtenis

1. 1
   Tel het aantal van alle kenmerkende en even waarschijnlijke uitkomsten van het experiment. Laat dat zo n.
   
2. 2
   Tel het aantal onderscheidende resultaten die het optreden van de gebeurtenis in kwestie vertegenwoordigen. Laat dat n _e zijn.
   
3. 3
   Bereken het resultaat van de deling _e n / n. Dat is de waarschijnlijkheid van de gebeurtenis.
   
4. 4
   Bijvoorbeeld: "Zoek de kans op het krijgen van een even getal na het werpen van een dobbelsteen"
   
   • Experiment: Rolling een eerlijke dobbelsteen
   • Event: Het krijgen van een even aantal
   • Bovenstaande stappen:
     1. Onderscheidend resultaten: 1, 2, 3, 4, 5, 6 zijn de resultaten, de verkiezingen n = 6
     2. Uitkomsten die het evenement: 2, 4, 6 zijn alle even getallen die je kunt krijgen, hun telling n _e = 3
     3. Waarschijnlijkheid: P = _e n / n = 3/6 = 0,5 of 1/2

     Waarschijnlijkheid van onafhankelijke gebeurtenissen die zich samen / gelijktijdig

     1. 1
        Vind de individuele waarschijnlijkheid van elke gebeurtenis op zich.
        
     2. 2
        Vermenigvuldig de individuele probabiliteiten de kans allen tezamen gebeuren voorbeeld.
        
     3. 3
        Voorbeeld: "Een matrijs wordt opgerold, een munt is gegooid, en een spinner met nummers 1 tot 5 wordt gesponnen Vind de kans op het krijgen van een 3, een kop en een 4 op de matrijs munt respectievelijk spinner tegelijk.. "
        
        1. Individuele waarschijnlijkheden:
           1. Het krijgen van een 3 bij het ​​rollen van een dobbelsteen: P ₁ = 1/6 (met de methode hierboven)
           2. Het krijgen van een hoofd als opgooien van een munt: P ₂ = 1/2
           3. Het krijgen van een 4 als een spinner wordt gesponnen: P ₃ = 1/5
        2. Waarschijnlijkheid: P = P ₁ * P ₂ * P ₃ = 1/6 * 1/2 * 1/5 = 1/60

        Waarschijnlijkheid van afhankelijke gebeurtenissen

        1. 1
           Bereken de kans van de eerste gebeurtenis. In bijna alle gevallen is er een of meer gebeurtenissen die andere gebeurtenissen afhankelijk zijn. Dit moet je eerste een om te berekenen. Het is onafhankelijk op zichzelf dus de eerste sectie is van toepassing.
           
        2. 2
           Identificeer de verandering die het eerste evenement plaats op het milieu van het experiment. Meestal in deze situaties, het optreden van de eerste gebeurtenis wordt beperkt of verhoogt het aantal mogelijke uitkomsten van het experiment.
           
        3. 3
           Bereken de kans van de tweede gebeurtenis (indien direct afhangt of volgt onmiddellijk de eerste gebeurtenis) volgens de methode van het eerste deel gezien de verandering die in 2.
           
        4. 4
           Blijven herhalen de stappen 2 en 3 voor de opeenvolgende gebeurtenissen, het identificeren van de veranderingen die door de vorige gebeurtenissen dan het berekenen van de waarschijnlijkheid van het nieuwe evenement in het licht van die verandering.
           
        5. 5
           Vermenigvuldig de waarschijnlijkheden u berekend vorige stappen, dat de waarschijnlijkheid van de afhankelijke gebeurtenissen geheel zijn.
           
        6. 6
           Bijvoorbeeld: "Er is een zakje met 5 groene knikkers, 2 rode en 3 blauwe degenen Wat zijn de kansen dat twee blauwe knikkers en daarna een rood marmer willekeurig worden gekozen uit de zak.? '
           
           1. Eerste evenement: het kiezen van een blauwe knikker (de eerste in de twee blauwe knikkers eerst te kiezen)
              1. Onderscheidend uitkomsten van het experiment: 5 groene + 2 rode + 3 blauw = 10 knikkers
              2. Uitkomsten die het evenement: 3 blauwe
              3. P ₁ = 3/10
           2. Wijzigen door gebeurtenis 1: aantal uitkomsten veranderd naar 5 groene + 2 rode + 2 blauw = 9 knikkers.
           3. Tweede geval: het kiezen van een blauwe marmer, met kans van 2 blauwe knikkers / 9 totaal = 2/9
           4. Wijzigen door event 2: aantal uitkomsten veranderd naar 5 groene + 2 rode + 1 blauw = 8 knikkers
           5. Derde geval: het kiezen van een rode marmer, met kans op 2 rode knikkers / 8 totaal = 1/4
           6. Totale waarschijnlijkheid: P _totaal = P ₁ * P ₂ * P ₃ = _3/10 * 2/9 * 1/4 = 6/360 = 1/60

           Termen en definities

           • Onafhankelijke gebeurtenissen: zijn twee gebeurtenissen die elkaar niet beïnvloeden doen. Bijvoorbeeld, is de rol van een dobbelsteen beïnvloeden het resultaat van de rol van een matrijs of het opgooien van een munt.
           • Afhankelijke gebeurtenissen: elkaar beïnvloeden. Als bijvoorbeeld een marmer genomen uit een zak en wordt niet vervangen, beïnvloedt de kans dat een bepaalde marmeren volgende zou worden opgesteld.
           • Het experiment: is de algemene context waarin de gebeurtenis plaatsvindt. Met andere woorden, is de reeks van acties die worden uitgevoerd op het milieu, welke tot het optreden van gebeurtenissen. Bijvoorbeeld, opgooien van een munt, het werpen van een dobbelsteen, het kiezen van een bal uit een zak of zelfs rijden naar een bepaalde toestand. Het hangt allemaal af van de context van het probleem.
           • Het milieu: is de set bronnen die worden gebruikt in het experiment. Bijvoorbeeld, een matrijs, twee munten, 6 groene ballen, een bestelwagen of zelfs een snelweg straat. Nogmaals, het hangt af van de context van het probleem.

           Tips

           • Neem extra zorg aan elk woord in de probleemstelling. Kijk uit voor de volgende woorden en begrijpen hun precieze betekenis in de context:
             • En, of, niet, maar
             • Dat voor elk voor elke
             • Behalve
             • "Minstens", "ten hoogste"
             • "Met", "zonder"
             • "Alleen als", "als en slechts als", "als"
           • Berekenen afhankelijke gebeurtenissen wordt gemakkelijk verknald. Het zou handig zijn als je een soort van een diagram te vestigen op de volgorde van de gebeurtenissen en het effect ieder doet voor het milieu van het experiment te vertegenwoordigen.