Trigonometrie is de tak van de wiskunde die zich bezighoudt met het bestuderen van driehoeken. Het is heel gemakkelijk te begrijpen als benaderd op de juiste manier. Dit artikel zal u helpen de slag te gaan leren trigonometrie.
Stappen
- 1Fris uw elementaire wiskundige vaardigheden. Deze omvatten de kennis van algebra en algebraïsche manipulatie evenals geometrie.
- Oefen algebraïsche manipulatie. Algebraïsche manipulatie is een zeer fundamentele vaardigheid die nodig is om een tak van wiskunde te studeren is.
- Leer om het onderwerp van een vergelijking te veranderen.
- Leer om lineaire en kwadratische vergelijkingen op te lossen.
- Leer om gelijktijdige lineaire vergelijkingen en lineaire / kwadratische paren van simultane vergelijkingen op te lossen.
- Leren van de basis geometrie. Geometrie is zeer nauw verwant aan driehoeksmeting en speelt een vitale rol in het oplossen van goniometrische problemen.
- Leer de eigenschappen van een cirkel.
- Leer de eigenschappen van het interieur en exterieur hoeken van polygonen waaronder driehoeken.
- Leer de drie verschillende soorten driehoeken dwz gelijkbenige, gelijkzijdige, en ongelijkzijdige.
- 2Beginnen met het bestuderen van rechthoekige driehoeken. Rechthoekige driehoeken zijn gemakkelijk te bestuderen en zal u een goed begrip van elementaire trigonometrie en de drie trigonometrische verhoudingen geven.
- Vertrouwd te maken met de drie zijden van een rechthoekige driehoek.
- De schuine zijde is de zijde tegenover de rechte hoek. Het is de grootste zijde van een rechthoekige driehoek.
- De beide andere zijden zijn de benen van de driehoek genoemd. Als je kiest voor elke hoek in de driehoek (naast de rechte hoek), zult u zien dat een been grenst aan de hoek, en het andere been is tegenover grenst> de hoek.
- Vertrouwd te maken met de drie trigonometrische verhoudingen, de basis van driehoeksmeting:
- De Sinus van een hoek is de verhouding van de lengte van de zijde tegenover het aan de lengte van de hypotenusa.
- De cosinus van een hoek is de verhouding van de lengte van de zijde grenzend aan het aan de lengte van de hypotenusa.
- De tangens van elke hoek is de verhouding van de sinus van de hoek met de cosinus van de hoek. Het wordt ook vaak beschouwd als de verhouding van de tegenover de aangrenzende. De eerste definitie is vooral van hulp bij het oplossen van goniometrische vergelijkingen en te bewijzen identiteit, terwijl de tweede is voldoende voor een fundamentele studie van driehoeksmeting.
- 3Gaan naar niet-rechthoekige driehoeken.. Omdat niet-rechthoekige driehoeken hebben geen rechte hoek (dat soort definitie), de drie trigonometrische verhoudingen speelt een kleinere rol (maar ze kunnen ook gebruikt worden in sommige gevallen). Integendeel, twee andere regels worden erg belangrijk: De sinus regel, en de cosinus regel. De volgende artikelen gaan over de voorschriften gedetailleerd.
- 4Leren hoeken in radialen gemeten. Radialen zijn een alternatief voor graden een manier van meten hoeken. In 180 o, er pi, of ongeveer 3,142, radialen. Radialen zijn vooral nuttig als het gaat om het onderzoeken van de eigenschappen van een cirkel, en worden ook gebruikt in de fysica de studie van golven en sinusvormige beweging.
- 5Leer de andere drie trigonometrische verhoudingen. Er zijn nog drie trigonometrische verhoudingen:
- Cosecans. Het is het omgekeerde van de sinus ie 1/sin gewoonlijk 'cosec' of 'CSC' genoemd.
- Secant. Het is het omgekeerde van de cosinus volksmond 'sec'.
- Cotangens. Het is het omgekeerde van de tangens gewoonlijk 'kinderbed' genoemd.
- 6Oefen het oplossen van goniometrische vergelijkingen. Goniometrische vergelijkingen zijn (je raadt het al) vergelijkingen met goniometrische functies. Goniometrische vergelijkingen meestal opgelost door het manipuleren van de vergelijking slechts een goniometrische verhouding bevatten. De volgende methoden worden gebruikt om een vergelijking met meer dan een trigonometrische rantsoen in een vergelijking die slechts een bevat converteren:
- Het verdelen van de hele vergelijking door een goniometrische term. Bijvoorbeeld, wanneer een vergelijking een term in sinus en een cosinus term in, verdeelt de hele vergelijking met cosinus. De term in sinus wordt een term in tan, en de term in cosinus wordt 1. Zo heb je een vergelijking alleen met tan.
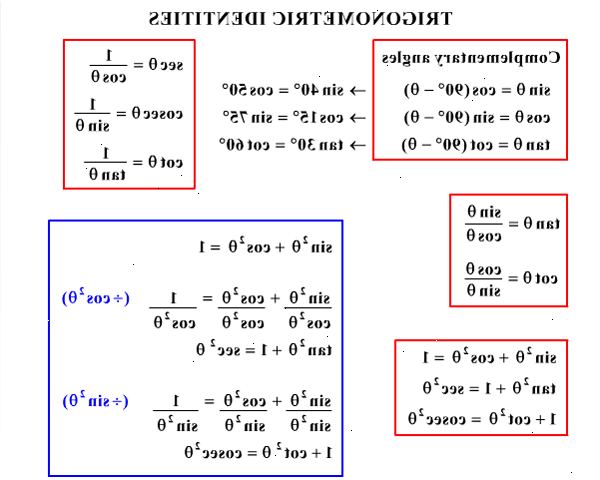
- Met een goniometrische identiteit. Trigonometrische identiteiten zijn "vergelijkingen" die altijd waar zijn. Twee goniometrische identiteiten worden hieronder geschreven:
sin 2 x + cos 2 x = 1
1 + tan 2 x = sec 2 x.
Dus als je een vergelijking met een term in sine 2 x en een in cosx had, zou je de term vervangen in sine 2 x met 1 - Cos 2 x uit de eerste identiteit hierboven. Dat zou resulteren in een kwadratisch in cosx, die u moet weten hoe op te lossen (zegt dus in de eerste stap).
- Vertrouwd te maken met de drie zijden van een rechthoekige driehoek.
- Oefen algebraïsche manipulatie. Algebraïsche manipulatie is een zeer fundamentele vaardigheid die nodig is om een tak van wiskunde te studeren is.
Tips
- Je hebt een wetenschappelijke rekenmachine.
- Kijk naar het antwoord sleutel als je vastzit.
- Als je problemen hebt, vraag een leraar of een goede leerling.
- Beoordelen algebra en meetkunde, vooral als je zwak bent.
- Koop een gradenboog.
- Vergeet niet dat de wiskunde is een manier van denken, niet een stel formules te leren. Ontwikkel je concepten en verscherp je denken vaardigheden door middel van het oplossen van problemen.
