Hoe de oppervlakte van een vierhoek vinden

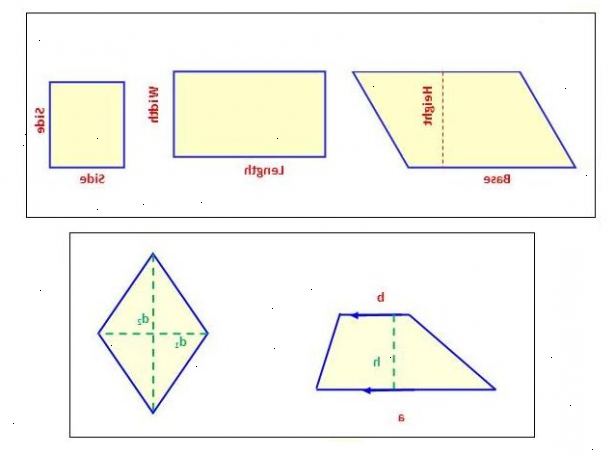
Vierkanten, rechthoeken en andere parallellogrammen

1. 1
   Weten wat een parallellogram is. Een parallellogram is elke vierhoek 2 paar evenwijdige zijden, waarbij de tegenoverliggende of tegenover zijden van gelijke lengte. Vierkanten, rechthoeken en ruiten zijn allemaal parallellogrammen.
   
2. 2
   Bereken de oppervlakte van een vierkant. Omdat elke zijde van een vierkant is van gelijke lengte, zult u gewoon vierkant de lengte van een zijde, de zogenaamde t. Gebruik de volgende vergelijking:
   
   • K = ^t2
3. 3
   Bereken de oppervlakte van een rechthoek. Om de oppervlakte van een rechthoek te vinden, moet 2 metingen: de breedte, of basis (de lange zijde van de rechthoek), en de lengte of hoogte (de korte zijde van de rechthoek). De formule is:
   
   • K = b * h
4. 4
   Bereken de oppervlakte van een ruit (of diamant). Om de oppervlakte van een ruit te vinden, moet u de hoogte, die wordt gedefinieerd als de loodrechte afstand tussen twee evenwijdige zijden kennen. Wees voorzichtig met deze - je kunt niet simpelweg vermenigvuldigen de ene kant door een aangrenzende kant. Als u nodig hebt om de hoogte van een parallellogram vinden, probeer het tekenen van de lijn voor de hoogte, zodat je een driehoek met een hoek van 90 graden. Nadat u de hoogte te verkrijgen, gebruik deze formule:
   
   • K = b * h

De oppervlakte van een trapezium

1. 1
   Weten wat een trapezium is. Een trapezoïde is een vierhoek met minstens 2 zijden die parallel lopen aan elkaar. Elk van de 4 zijden van een trapezium kan een andere lengte. Er zijn twee verschillende manieren waarop u de oppervlakte van een trapezium vinden, afhankelijk van welke informatie je hebt.
   
2. 2
   Zoek de hoogte van het trapezium. De hoogte van een trapezium is de loodrechte lijn verbindt de bovenste basislijn en de onderste basislijn, en je zult het nodig hebben voor zowel de omgeving vergelijkingen. Hierdoor wordt dezelfde lengte als een van de zijden niet, omdat elke zijde schuin opgemerkt. Hier ziet u hoe de hoogte vinden:
   
   • Vind de kortere basis. Plaats je potlood op de hoek tussen die basislijn en een van de zijkanten, en trek een lijn recht omhoog of omlaag om de andere basislijn. Je moet een driehoek met een hoek van 90 graden hebben gecreëerd.
   • Gebruik driehoeksmeting om de hoogte te bepalen. Bijvoorbeeld, als jij de lengte van de zijde en dat er een hoek van 90 graden in de driehoek, kan aannemen dat de cosinus van 90 graden hoogte gedeeld door de lengte van de zijde gelijk.
3. 3
   Bereken de oppervlakte van het trapezium met de hoogte. Als u de hoogte van de trapezoïde, en de lengte van beide bases, de volgende vergelijking:
   
   • K = (a + b) / 2 * h
4. 4
   Bereken de oppervlakte van een trapezium met de midsegment. De midsegment zou een lijn die evenwijdig aan de onderste en bovenste lijnen van het trapezium loopt, en moet een lengte die precies tussen hen zijn. Hier is hoe te werken met een midsegment:
   
   • Zoek de midsegment. Om de midsegment m worden, zoals de gemiddelde zijden a en b (of de bovenste en onderste "bases" van de trapezoïde). Met deze formule: m = (a + b) / 2. Nu dat je de midsegment, kunt u dit vermenigvuldigen met de hoogte om het gebied te vinden. Gebruik de volgende vergelijking:
   • K = m * h

Het vinden van de oppervlakte van een vlieger

1. 1
   Weten wat een vlieger is. Een vlieger wordt gedefinieerd als een geometrische vorm die 2 paren van gelijke lengte zijden naast elkaar, lijkt op een echte kite. Er zijn twee verschillende manieren om de omgeving te vinden, afhankelijk van welke informatie je hebt.
   
2. 2
   Vind het zijn van een vlieger met de lengten van de zijden. Als u de lengten van twee verschillende kanten, evenals de hoek de hoek tussen de zijden Gebruik formule waarbij de hoek theta (θ):
   
   • K = (a * b) * sinθ
3. 3
   Bereken de oppervlakte van een vlieger met diagonalen. Een diagonaal is de rechte lijn tussen twee tegenovergestelde hoeken van de vlieger. Elke vlieger heeft 2 diagonalen.
   
   • Bepaal de lengte van een diagonaal. Trek een lijn van de ene kant van de vlieger naar de andere. Je hebt nu twee driehoeken. Gebruik, bepalen de lengte van de diagonaal. (Vergeet niet dat alle drie de hoeken in een driehoek moet toevoegen tot 180 graden.)
   • Als je eenmaal hebt bedacht de eerste diagonaal, maken gebruik van dezelfde principes om de lengte van de andere bepaalt. Gebruik deze vergelijking om waar p en q zijn de lengtes van de diagonalen bepalen:
   • K = (p * q) / 2

Met een algemene vergelijking

1. 1
   Gebruik een algemene vierhoek gebied vergelijking. Er zijn formules die u kunt gebruiken om te achterhalen van de oppervlakte van een vierhoek, ongeacht zijn vorm. Hier is de meest voorkomende, die de principes van driehoeksmeting gebruikt:
   
   • Als K is de totale oppervlakte van de vierhoek, a, b, c en d zijn de lengten van de zijden 4, A is de hoek (in graden) tussen de zijden a en d, en C is de hoek (in graden) tussen partijen b en c, dan:
     • K = (0.5a * d) * sin A + (0.5b * c) * sin C
     • Als je probeert om de oppervlakte van een parallellogram, waarbij de tegenovergestelde hoeken gelijk vinden, de vergelijking reduceert tot K = 0.5 (ad + bc) * sin A.