Het product correlatiecoëfficiënt laat u uit te werken van de lineaire afhankelijkheid van twee variabelen (aangeduid als x en y). Een voorbeeld in de economie kan zijn dat u de eigenaar van een restaurant. Voor elke 10e klant u de tijd dat hij verbleef in uw restaurant (x, in minuten) en het bedrag te besteden (y, in dollars) opnemen. Is het in het algemeen zo dat de lange blijvers zijn ook de grotere spenders? Dit zou een positieve correlatie te zijn. Of is het eigenlijk andersom, bijvoorbeeld hoe rijker de cliënt hoe minder tijd hij neemt voor zijn lunch? Dit zou een negatieve correlatie te zijn. Om enig licht te werpen op dit mysterie kunt u de PMCC berekenen.
Stappen
- 1Verwijder onvolledige paren. In de volgende stap alleen waarnemingen waarbij zowel x en y bekend. Echter niet observaties sluiten, alleen maar omdat een van de waarden gelijk aan nul.
- 2Vat de gegevens in de waarden nodig voor de berekening. Deze zijn:
- n - het aantal data.
- Σx - de som van alle x-waarden.
- Σx 2 - de som van de kwadraten van de x-waarden.
- Σy - de som van alle y-waarden.
- Σy 2 - de som van de kwadraten van de y-waarden.
- Σxy - de som van x iedere waarde vermenigvuldigd met de overeenkomstige y-waarde.
- 3Bereken s xy, s xx en yy s met behulp van deze waarden.
- S xy = Σxy-(ΣxΣy ÷ n)
- S xx = Σx 2 - (ΣxΣx ÷ n)
- S yy = Σy 2 - (ΣyΣy ÷ n)
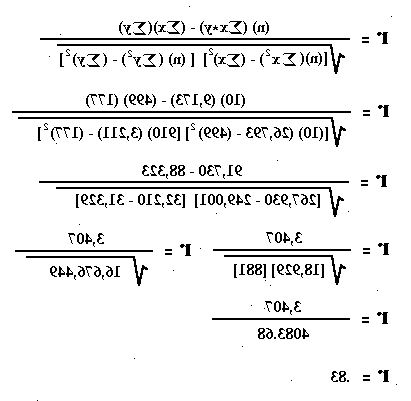
- 4Steek deze waarden in de onderstaande vergelijking om het product correlatiecoëfficiënt (r) te berekenen. De waarde moet liggen tussen 1 en -1.
- Een waarde dicht bij 1 betekent een sterke positieve correlatie. (Hoe hoger de x, hoe hoger de y).
Tips
- Maak altijd een scatterplot. Anders kunt u uw ontdekking missen omdat het product correlatiecoëfficiënt neemt alleen rechte lijnen te houden in het bedrijf van het voorspellen van y van x.
- Dit is de reden waarom veel van de vragenlijsten hebben dezelfde vragen, waardoor ze ongelooflijk saai te beantwoorden. De onderzoekers weten vaak veel over vraag x en y vraag, maar ze weten nog niet hoe ze gerelateerd zijn.
Waarschuwingen
- Voordat u verklaart dat twee variabelen gecorreleerd zijn zorg ervoor dat de correlatiecoëfficiënt is statistisch significant. Dat wil zeggen dat de berekende correlatiecoëfficiënt is waarschijnlijk een gevolg van toeval zijn. Bijvoorbeeld al je 3 punten kan vaststellen op dezelfde lijn, heeft dit een coëfficiënt van +1 of -1, maar het zou nog steeds onduidelijk.
- Als de coëfficiënt niet significant het algemeen geen zin rapporteren van waarde.
- Wanneer de correlatie is significant u nog niet bewezen dat een variabele "oorzaken" van de andere. Je hebt slechts gecontroleerd dat de kennis van de waarde van x kan helpen in zekere mate in het voorspellen van de waarde van y en andersom.
