Dit zal u instrueren over hoe je tweedegraads veeltermen factor. Een polynoom bevat een variabele (x) verheven tot een macht, die bekend staat als een diploma, en een aantal voorwaarden en / of constanten. Om een polynoom factor betekent de uitdrukking breken in meer hanteerbare brokken die met elkaar worden vermenigvuldigd. Deze vaardigheden zijn Algebra I en hoger, en dus kan moeilijk te begrijpen zijn als je wiskunde vaardigheden zijn niet op dit niveau.
In dit artikel worden de termen verwezen naar de standaardvorm van een kwadratische vergelijking:
ax 2 + bx + c = 0
Stappen
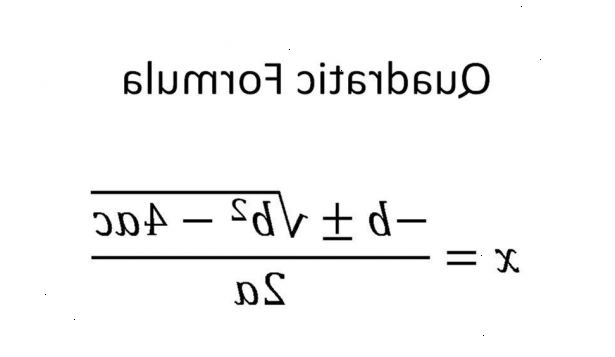
- 1Stel uw expressie. Bestel de nummers van hoogste naar laagste vermogen en vervolgens factor uit de grootste gemene deler als deze bestaat.
6 + 6x 2 + 13x
6x 2 + 13x + 6 - 2Vind de ingecalculeerd vorm via een van de volgende methoden.
(2x + 3) (3x + 2) - 3Controleer uw werk door vermenigvuldiging van de factoren met folie. Dan combineer zoals termen en je bent klaar!
(2x + 3) (3x + 2)
6x 2 + 4x + 9x + 6
6x 2 + 13x + 6
Trial and error methode
Als je een vrij eenvoudige polynomiale, zult u in staat te achterhalen van de factoren zelf. OPMERKING: Met deze methode kan niet zo eenvoudig als wanneer factoring ingewikkelder trinomials.
Voorbeeld: 3x 2 + 2x - 8
- 1Van alle factoren van het een term en de c term.
a = 3 factoren: 1 en 3
c = -8 factoren: 2 en 4 of 1 en 8 - 2Schrijf twee sets haakjes met lege ruimtes als dit:
(X) (x) - 3Vullen de ruimtes voor de x met een paar van de mogelijke factoren een waarde. Er is maar een mogelijkheid voor ons voorbeeld:
( 3x) ( 13x) (x)
- 4Vul de twee ruimten na x met een paar elementen voor de constante. Laten we zeggen dat we kiezen (3x 8) (x 18) (x).
- 5Beslissen wat borden moet tussen de x en de nummers. Hier is een gids:
Als ax 2 + bx + c dan (x + h) (x + k)
Als ax 2 - bx - c of ax 2 + bx - c toen (x - h) (x + k)
Als ax 2 - bx + c dan (x - h) (x - k)
Voor ons voorbeeld 3x 2 + 2x - 8 dus (x - h) (x + k)
We zullen moeten raden als voor de rest. (3x + 8) (x - 1) - 6Test uw keuze door te vermenigvuldigen (gebruik FOLIE) de twee haakjes aan elkaar. Als de middelste term is niet op zijn minst de juiste waarde (zonder rekening te houden positief of negatief) heb je de verkeerde c factoren gekozen.
(3x + 8) (x - 1)
3x 2 - 3x + 8x - 8
3x 2 + 5x - 8 ≠ 3x 2 + 2x - 8 - 7Verwissel uw keuzes indien nodig. In ons voorbeeld, laten we proberen 2 en 4 in plaats van 1 en 8: (3x + 2) (x - 4)
- Nu onze c term is een -8.
- Maar onze Outside / Inside combo is-12x en 2x, die niet zal combineren om de juiste b termijn van 2 x maken.
- 8De volgorde om te keren indien nodig. Laten we proberen het verplaatsen van de 2 en 4 rond: (3x + 4) (x - 2)
- c term is nog steeds goed.
- Buiten / Binnen combo is-6x en 4x. Als we ze combineren, krijgen we redelijk dicht bij de 2x waren we streven naar --- juiste hoeveelheid, verkeerd teken.
- 9Double-check uw borden indien nodig. We gaan aan de stok met dezelfde volgorde, maar swap die men heeft het aftrekken: (3x - 4) (x + 2)
- c term is nog steeds goed.
- Buiten / Binnen combo is nu 6x en-4x. Deze vormt samen met de positieve 2x maken van het oorspronkelijke probleem, zodat deze de juiste factoren.
Decompositiemethode
Als de nummers zijn groot of ben je gewoon moe van giswerk gebruiken deze methode.
Voorbeeld: 6x 2 + 13x + 6
- 1Vermenigvuldig het een term (6 in het voorbeeld) door de c term (ook 6 in het voorbeeld).
6 • 6 = 36 - 2Zoek twee getallen die vermenigvuldigd gelijk dit nummer (36) en optellen tot de b term (13) te zijn.
4 • 9 = 36 4 + 9 = 13 - 3De plaats van de twee nummers je in deze vorm als k en h (volgorde maakt niet uit): ax 2 + kx + hx + c
6x 2 + 4x + 9x + 6 - 4Factor de polynoom door ze te groeperen. Organiseren de vergelijking, zodat u kunt nemen uit de grootste gemene deler van de eerste twee termen en de laatste twee termen. Beide ingecalculeerd groepen moet hetzelfde zijn. Voeg de GCF's elkaar en omsluiten ze tussen haakjes naast de ingecalculeerd groep.
6x 2 + 4x + 9x + 6
2x (3x + 2) + 3 (3x + 2)
(2x + 3) (3x + 2)
Triple play methode
Het is zeer vergelijkbaar met de ontleding methode, maar het is eenvoudiger.
Voorbeeld: 8x 2 + 10x + 2
- 1Vermenigvuldig het een term (8 in het voorbeeld) door de c term (2 in dit voorbeeld).
8 • 2 = 16 - 2Zoek de twee getallen waarvan het product is dit nummer (16) en waarvan de som gelijk is aan de term b (10).
2 • 8 = 16 8 + 2 = 10 - 3Neem deze twee getallen (die we zullen noemen h en k), en vervangen ze in deze uitdrukking:
(Ax + h) (ax + k)
een
(8x + 8) (8x + 2)
8 - 4Kijken om te zien welke van de twee haakjes termen in de teller is gelijkmatig deelbaar door een {in dit voorbeeld is het (8x + 8)}. Verdeel deze term door een en laat het andere als is.
(8x + 8) (8x + 2)
8
Antwoord: (x + 1) (8x + 2) - 5Neem de GCF (indien aanwezig) van een of beide haakjes.
(X + 1) (8x + 2)
2 (x + 1) (4x + 1)
Verschil van twee kwadraten
- 1Factor een GCF als je nodig hebt om.
27x 2-12
3 (9x 2 - 4) - 2Bepaal of uw vergelijking is een verschil van kwadraten. Het moet twee termen en je moet in staat zijn om de vierkantswortel van de termen gelijkmatig nemen.
√ (9x 2) = 3x en √ (4) = 2 (merk op dat we hebben weggelaten het minteken) - 3Doe de a en c waarden uit uw vergelijking in deze uitdrukking:
(√ (a) + √ (c)) (√ (a) - √ (c))
3 [(√ (9x 2) + √ (4)) (√ (9x 2) - √ (4))]
3 [(3x + 2) (3x - 2)]
Met behulp van de kwadratische formule
Als al het andere faalt en de vergelijking zal niet gelijkmatig factor Gebruik de kwadratische formule.
Voorbeeld: x 2 + 4 x 1 +
- 1Steek de overeenkomstige waarden in de kwadratische formule:
x =-b ± √ (b 2 - 4ac)
2a
x = -4 ± √ (02-04 april • 1 • 1)
2 • 1 - 2Lossen voor x. Je moet je twee x-waarden.
x = -4 ± √ (16-4)
2
x = -4 ± √ (12)
2
x = -4 ± √ (4 • 3)
2
x = -4 ± 2 √ (3)
2
x = -2 ± √ (3)
x = -2 + √ (3) of x = -2 - √ (3) - 3Steek de x-waarden (h en k) in deze uitdrukking: (x - h) (x - k)
(X - (-2 + √ (3)) (x - (-2 - √ (3))
(X + 2 + √ (3)) (x + 2 - √ (3))
Met behulp van een rekenmachine
Deze aanwijzingen zijn voor een TI grafische rekenmachine. Deze zijn vooral handig in gestandaardiseerde tests.
- 1Voer uw vergelijking in de [y =] scherm.
y = x 2 - x - 2 - 2Druk op [grafiek]. Je moet een vloeiende boog te zien.
- 3Lokaliseren waar de boog snijdt de x-as. Dit zijn de x-waarden.
(-1, 0), (2, 0)
x = -1, x = 2- Als je ze niet kunt identificeren door gezicht drukt u op [2] en daarna [TRACE]. Druk op [2] of "nul" te selecteren. Schuif de cursor naar links van een kruisen en druk op [ENTER]. Schuif de cursor rechts van een kruisen en druk op [ENTER]. Schuif de cursor zo dicht mogelijk bij het kruisen en druk op [ENTER]. De calculator zal de x-waarde te vinden. Doe dit voor de andere kruisen ook.
- 4Steek de x-waarden (h en k) in deze uitdrukking: (x - h) (x - k)
(X - (-1)) (x - 2)
(X + 1) (x + (-2)) grote plus toevoegen aan de gemeenschappelijke factor
Tips
- Als u een TI-84 rekenmachine (grafische) is er een programma met de naam SOLVER dat een vierkantsvergelijking zal oplossen. Het zal ook het oplossen van eventuele andere polynoom.
- Als u meegewogen uw polynoom met de kwadratische formule en kreeg een antwoord met een radicale, wilt u misschien de x-waarden om te zetten in fracties om het te controleren.
- Als een term heeft geen coëfficiënt zoals geschreven, de coëfficiënt 1.
x 2 = 1x 2 - Wanneer een term niet bestaat de coëfficiënt is 0. Het zal nuttig zijn om de vergelijking herschrijven als dit gebeurt.
x 2 + 6 = x 2 + 6 + 0x - Uiteindelijk zul je in staat zijn om trial and error doen in je hoofd. Tot die tijd, zorg ervoor om het te schrijven.
Waarschuwingen
- Als je leert dit concept in een rekenles, let op wat je leraar adviseert en niet gewoon gebruik maken van uw favoriete methode. Je docent kan u vragen om een specifieke methode te gebruiken op de test of niet toestaan grafische rekenmachines.
Dingen die je nodig hebt
- Potlood
- Papier
- Vierkantsvergelijking (ook wel een 2e graads polynoom)
- Grafische rekenmachine (optioneel)
