Na het verzamelen van gegevens, vaak het eerste wat je hoeft te doen is te analyseren. Dit houdt meestal het vinden van het gemiddelde, de standaarddeviatie en de standaardfout van de gegevens. Dit artikel zal u tonen hoe het moet.
Stappen
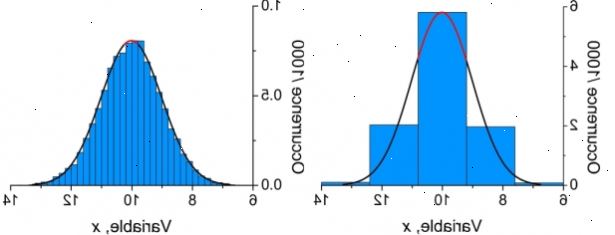
Gegevens
- 1Verkrijgen van een reeks getallen die u wilt analyseren. Deze informatie wordt aangeduid als een monster.
- Zo wordt een test gegeven tot een klasse van 5 studenten en de testresultaten zijn 12, 55, 74, 79 en 90.
- Zo wordt een test gegeven tot een klasse van 5 studenten en de testresultaten zijn 12, 55, 74, 79 en 90.
De gemiddelde
- 1Bereken het gemiddelde. Tel alle getallen en delen door de omvang van de populatie:
- Gemiddelde (μ) = ΣX / N, waarbij de som Σ (toevoeging) teken, x i is elk individueel nummer, en N is de populatiegrootte.
- In het bovenstaande geval, de gemiddelde μ gewoon (12 +55 +74 +79 +90) / 5 = 62.
- Gemiddelde (μ) = ΣX / N, waarbij de som Σ (toevoeging) teken, x i is elk individueel nummer, en N is de populatiegrootte.
De standaarddeviatie
- 1Bereken de standaarddeviatie. Dit vertegenwoordigt de spreiding van de bevolking.
- Voor het gegeven voorbeeld, de standaarddeviatie is sqrt [((12-62) ^ 2 + (55-62) ^ 2 + (74-62) ^ 2 + (79-62) ^ 2 + (90-62) ^ 2) / (5)] = 27.4. (Merk op dat als dit was de steekproef standaardafwijking, zou je delen door n-1, de steekproefomvang minus 1.)
- Voor het gegeven voorbeeld, de standaarddeviatie is sqrt [((12-62) ^ 2 + (55-62) ^ 2 + (74-62) ^ 2 + (79-62) ^ 2 + (90-62) ^ 2) / (5)] = 27.4. (Merk op dat als dit was de steekproef standaardafwijking, zou je delen door n-1, de steekproefomvang minus 1.)
De standaardafwijking van het gemiddelde
- 1Bereken de standaard fout (van het gemiddelde). Dit vertegenwoordigt hoe goed het steekproefgemiddelde benadert de bevolking betekenen. Hoe groter de steekproef, hoe kleiner de standaardfout, en hoe dichter de steekproef gemiddelde benadert de bevolking betekenen. Doe dit door het verdelen van de standaarddeviatie van de vierkantswortel van N, de steekproefomvang.
- Dus het bovenstaande voorbeeld, als dit een steekproef van 5 studenten uit een klasse van 50 en 50 studenten had een standaarddeviatie van 17 (σ = 21), de standaardfout = 17/sqrt (5) = 7,6.
- Dus het bovenstaande voorbeeld, als dit een steekproef van 5 studenten uit een klasse van 50 en 50 studenten had een standaarddeviatie van 17 (σ = 21), de standaardfout = 17/sqrt (5) = 7,6.
Tips
- Berekening van de gemiddelde, standaarddeviatie en standaardfout zijn het meest bruikbaar voor de analyse van normaal verdeelde gegevens. Een standaarddeviatie rond de centrale tendens beslaat ongeveer 68 procent van de data, 2 standaardafwijking 95 procent van de data, en 3 standaarddeviatie 99,7 procent van de data. De standaardfout wordt kleiner (smaller spread) als de steekproefomvang toeneemt.
- Een eenvoudig te gebruiken online standaarddeviatie rekenmachine gebruiken
Waarschuwingen
- Controleer je wiskunde zorgvuldig. Het is heel gemakkelijk om fouten te maken of voer nummers verkeerd.
