Hoe te afgeleiden nemen in calculus

1. 1
   Begrijp de afgeleide notatie. De volgende twee notaties zijn de meest voorkomende, maar er zijn talloze anderen die kan worden gevonden op Wikipedia.
   
   • Leibniz Notation Deze notatie komt het meest voor bij de vergelijking gaat y en x. dy / dx betekent letterlijk "de afgeleide van y naar x." Het kan nuttig zijn om te denken als Ay / Ax voor waarden van x en y die zijn oneindig verschillend van elkaar. Deze verklaring leent zich tot het uiterste definitie van een derivaat: lim _{h-> 0} (f (x + h)-f (x)) / h. Bij het ​​gebruik van deze notatie voor de tweede afgeleide, moet je schrijven: d ² y / dx ^2.
   • Lagrange Notatie De afgeleide van een functie f wordt ook geschreven als f '(x). Deze notatie wordt uitgesproken als "f prime van x". Deze notatie is korter dan Leibniz notatie, en is nuttig als we kijken naar de afgeleide als functie. Tot hogere orde afgeleiden vormen, voegt een ander "'" naar "f", dus de tweede afgeleide zou zijn f'' (x).
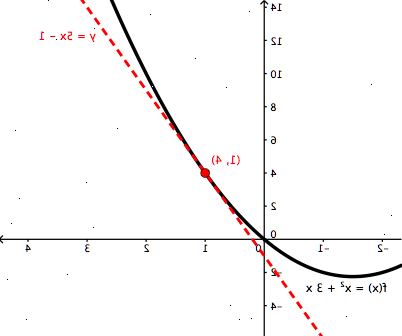
2. 2
   Begrijpen wat het derivaat is, en waarom het wordt gebruikt. Allereerst, de helling van een lineaire grafiek te vinden, worden twee punten op de lijn, en de coördinaten en aangesloten op de vergelijking (y ₂ - _y1) / (x ₂ - x _1). Dit kan echter alleen worden gebruikt met lineaire grafieken. Voor kwadratische vergelijkingen en hoger, zal de lijn worden gebogen, zodat het nemen van het "verschil" van twee punten zullen niet nauwkeurig zijn. Om de helling van de raaklijn aan een gebogen grafiek vinden, worden twee punten genomen, en aangesloten op de standaard vergelijking voor het vinden van de helling van een kromme grafiek: [f (x + dx) - f (x)] / dx. Dx staat voor "delta x," dat het verschil tussen de twee x-coördinaten van de twee punten van de grafiek. Merk op dat deze vergelijking gelijk is aan _(y2 - _y1) / (x ₂ - x _1), op een afwijkende vorm. Omdat het reeds bekend is dat de resultaten onnauwkeurig zijn, wordt een indirecte benadering toegepast. Om de helling van de tangens bij (x, f (x)), moet dx benaderen 0, zodat de twee punten die werden genomen samenvoegen in een punt. U kunt echter niet delen door 0, dus nadat u de stekker in de waarden van de twee punten is, moet u factoring en andere methoden te gebruiken om te annuleren van dx in de bodem van de vergelijking. Zodra je dat gedaan hebt, stel dx naar 0 en op te lossen. Dit is de helling van de raaklijn in (x, f (x)). De afgeleide van een vergelijking van de algemene vergelijking voor het vinden van de helling van een raaklijn op een grafiek. Dit lijkt misschien erg ingewikkeld, maar er zijn enkele voorbeelden hieronder, die zal helpen verduidelijken hoe het derivaat te verkrijgen.
   

Expliciete differentiatie

1. 1
   Gebruik expliciete differentiatie wanneer uw vergelijking heeft al y naar een kant.
   
2. 2
   Steek de vergelijking in de vergelijking [f (x + dx) - F (x)] / dx. Als bijvoorbeeld de vergelijking was y = x ^2, zou het derivaat worden [(x + dx) ² - x ^2] / dx.
   
3. 3
   Uitbreiden en factor uit dx om de vergelijking te vormen [dx (2x + dx)] / dx. Nu kunt u annuleert de twee dx's op de boven-en onderkant. Het resultaat is 2x + dx, en wanneer dx 0 nadert, de afgeleide is 2x. Dit betekent dat de helling van een raaklijn aan de grafiek y = x ² 2x. Sluit gewoon de x-waarde van het punt waar u wilt de helling te vinden.
   
4. 4
   Leerpatronen voor het afleiden van gelijkaardige soorten vergelijkingen. Hieronder zijn een paar.
   
   • De afgeleide van een macht is de macht keer de waarde tot de macht minus 1. Bijvoorbeeld, de afgeleide van ⁵ x 5 x ⁴ is, en de afgeleide van x ^3,5 is 3.5x ^2.5. Als er al een aantal in de voorkant van x, maar vermenigvuldig het met de macht. Bijvoorbeeld, de afgeleide van 3x ⁴ is 12x ^3.
   • De afgeleide van een constante nul. Dus de afgeleide van 8 is 0.
   • De afgeleide van een som is de som van de afzonderlijke derivaten. Bijvoorbeeld, de afgeleide van x ³ + 3x ² is 3x ² + 6x.
   • De afgeleide van een product is de eerste factor maal de afgeleide van de tweede factor plus de tweede factor maal de afgeleide van de eerste. Bijvoorbeeld, de afgeleide van x ³ (2x + 1) is ³ x (2) + (2x + 1) 3x ² die 8x ³ + 3x ² gelijk.
   • De afgeleide van een quotiënt (zeg, f / g) is [g (afgeleide van f) - f (afgeleide van g)] / g ^2. Bijvoorbeeld, de afgeleide van (x ² + 2x - 21) / (x - 3) is (x ² - 6x + 15) / (x - 3) ^2.

Impliciete differentiatie

1. 1
   Gebruik impliciet afleiden wanneer je vergelijking niet gemakkelijk kan worden geschreven met een y op alleen een kant. Zelfs als je hebt het toch wel met y aan de ene kant, zou computergebruik dy / dx vervelend zijn. Hieronder is een voorbeeld van hoe je dit soort vergelijking zou oplossen.
   
2. 2
   In dit voorbeeld, x ² y + 2y ³ = 3x + 2y, vervang y met f (x), dus je zult herinneren dat y is eigenlijk een functie. De vergelijking wordt dan x ² f (x) + 2 [f (x)] ³ = 3x + 2 f (x).
   
3. 3
   Om de afgeleide van de volgende vergelijking, differentiëren (een groot woord voor het vinden van het derivaat) aan beide zijden van de vergelijking van x. De vergelijking wordt dan ² x f '(x) + 2XF (x) + 6 [f (x)] ² f' (x) = 3 + 2f '(x).
   
4. 4
   Vervang f (x) met y weer. Wees voorzichtig niet om hetzelfde te doen met f '(x), die anders is dan f (x).
   
5. 5
   Lossen voor f '(x). Het antwoord op dit voorbeeld komt uit op (3 - 2xy) / (x ² + 6j ² - ^2).
   

Hogere orde afgeleiden

1. 1
   Het nemen van een hogere orde afgeleide van een functie betekent gewoon dat je de afgeleide van de afgeleide (voor orde van 2) te nemen. Bijvoorbeeld, als deze vraagt ​​om de derde orde afgeleide te nemen, neem dan gewoon de afgeleide van de afgeleide van de afgeleide. Voor sommige vergelijkingen, zal de hogere orde afgeleiden tot 0.
   

De kettingregel

1. 1
   Als y een differentieerbare functie van z en z een differentieerbare functie van x, y een samengestelde functie van x en de afgeleide van y naar x (dy / dx) is (dy / du) * (du / dx). De kettingregel kunnen ook samengestelde macht vergelijkingen, zoals deze: (2x ⁴ - x) ^3. Om de afgeleide vinden, denk maar als het product regel. Vermenigvuldig de vergelijking door de kracht en verminderen de macht door 1. Vermenigvuldig de vergelijking van de afgeleide van de binnenkant van het vermogen (in dit geval, 2x ^ 4 - x). Het antwoord op dit probleem komt naar 3 (2x ⁴ - x) ² (8x ^3-1).