Hoe je wortels vermenigvuldigen

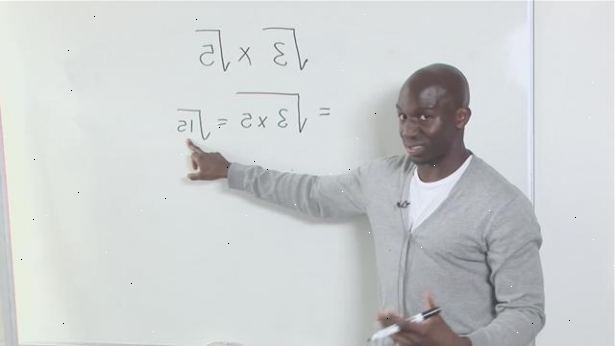
Vermenigvuldigen met een enkele termijn wortels zonder coëfficiënten

1. 1
   Ken uw woordenschat:
   • De coëfficiënt is de volledige getal voor de radicale symbool.
   • De radicand is het nummer waaronder de radicale symbool.
2. 2
   Probeer de radicands vereenvoudigen.
   • Stel je voor dat je de vierkantswortel van 15 maal de wortel van 5 vermenigvuldigen.
   • Noch 15 noch 5 bevat geen perfecte vierkanten. Daarom kunt u niet vereenvoudigen de radicand.
3. 3
   Vermenigvuldig de radicands. Bijvoorbeeld, de vierkantswortel van 5 maal de wortel van 15 is gelijk aan de vierkantswortel van 75 omdat 5 * 15 = 75.
4. 4
   Vereenvoudig de radicands om alle factoren die perfecte vierkanten zijn te verwijderen.
   • Kijk naar het resultaat en probeer factor uit elke vierkante wortels. Bijvoorbeeld, als de radicand is 75, kunt u factor de vierkantswortel van 75 in een nieuwe uitdrukking: de vierkantswortel van 25 maal de vierkantswortel van 3.
   • Herschikken van de expressie. Sinds de vierkantswortel van 25 is gelijk aan 5, dan is de vierkantswortel van 75 wordt 5 maal de vierkantswortel van 3.

Vermenigvuldig vierkante wortels die coëfficiënten betrekken

1. 1
   Stel je voor dat je de vierkantswortel van 18 maal de wortel van 6 vermenigvuldigen.
2. 2
   Begin met het vereenvoudigen van de radicands.
   • Terwijl 6 bevat geen perfecte vierkanten, 18 is gelijk aan 9 * 2. 9 is een perfect vierkant, dus herschrijven de vierkantswortel van 18 als de vierkantswortel van 9 maal de vierkantswortel van 2.
   • Herschrijven van de volledige uitdrukking. De uitdrukking wordt de vierkantswortel van 9 maal de wortel van 2 maal de vierkantswortel van 6.
   • Herschrijf de vierkantswortel van 9 in zijn eenvoudigste vorm, de vierkantswortel van 9 is gelijk aan 3. Uw uitdrukking luidt nu 3 maal de wortel van 2 maal de vierkantswortel van 6.
3. 3
   Vermenigvuldig de radicands. Uw uitdrukking zal nu zeggen dat 3 maal de vierkantswortel van 12 want 6 * 2 = 12.
4. 4
   Factor uit een ander perfect vierkant. 12 = 4 * 3 en 4 is een perfect vierkant.
   • Herschrijf de expressie. Het zou nu lezen 3 maal de vierkantswortel van 4 maal de vierkantswortel van 3.
   • Vereenvoudig uw voorwaarden. Sinds de vierkantswortel van 4 evenaart 2, moet de uitdrukking zeggen nu 3 maal 2 maal de vierkantswortel van 3.
5. 5
   Vermenigvuldig de coëfficiënten. 3 * 2 gelijk aan 6. Daarom is uw definitieve antwoord is gelijk aan 6 keer de vierkantswortel van 3.

Vermenigvuldigen van een binomiaal bevattende vierkantswortels

1. 1
   Gebruik maken van de FOLIE methode om de uitdrukkingen vermenigvuldigen. Dit betekent dat aan de eerste voorwaarden, dan is de uiterlijke voorwaarden, dan is de innerlijke voorwaarden en vervolgens de laatste termen vermenigvuldigen.
   • Schrijf de vermenigvuldiging volledig.
   • Vermenigvuldig alle termen samen, waaronder zowel radicands en coëfficiënten.
2. 2
   Factor out perfecte vierkanten en de expressie te vereenvoudigen.
3. 3
   Optellen of aftrekken wortels door het combineren van soortgelijke termen.