We hebben allemaal wel te kampen met problemen in de algebra genaamd "woord problemen." Een typisch woord probleem met zich meebrengt mengoplossingen van bepaalde sterke punten om een bepaalde hoeveelheid van het mengsel te krijgen op een gewenste sterkte. In dit artikel vindt u een algemene techniek voor het oplossen van dergelijke problemen te leren.
Stappen
- 1Om de stappen uit te leggen, zullen we een specifiek voorbeeld probleem te gebruiken:
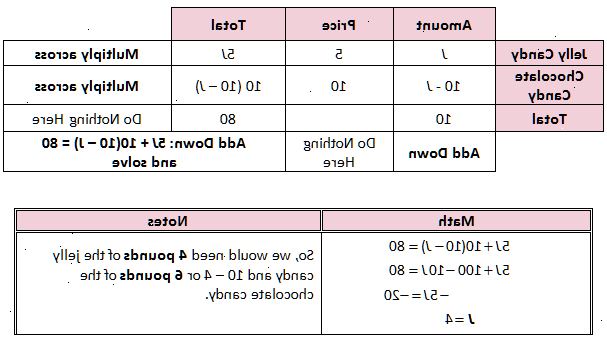
- 2Hypatia heeft 20% en 15% oplossingen van zout (zout) oplossing. Hoeveel van elk moet ze mengen tot 5 liter van 18% zoutoplossing te krijgen?
- 3Organiseer uw gegevens. Over het algemeen heb je drie percentages, twee onbekende hoeveelheden, en een bekende hoeveelheid. De gebruikelijke algemene structuur:
- 4Bepalen welke informatie de uiteindelijke sterkte en hoeveelheid vertegenwoordigt. In ons voorbeeld wordt het eindproduct verondersteld 5 liter 18% zoutoplossing.
- 5De plaats van de informatie met betrekking tot de uiteindelijke sterkte en hoeveelheid.
- 6De plaats van de andere twee percentages. Het maakt niet uit welke je voor A en die voor B.
- 7Kies een variabele voor een van de onbekende bedragen. Het maakt niet uit welke je kiest. Voor dit probleem, kiezen we x om het bedrag van 20% oplossing vertegenwoordigen.
- 8Druk het bedrag van de andere oplossing te gebruiken. Omdat we weten dat de bedragen moeten optellen tot 5 liter, en we hebben al x gekozen voor de 20%-oplossing, het bedrag van de andere oplossing is 5 - x.
- 9Beëindig de vermenigvuldiging is dat na de gelijk-teken.
- 10Verdeel de vermenigvuldiging over de hoeveelheid 5 - x.
- 11Los de rest van de vergelijking.
- 12Interpreteer het antwoord. We kozen voor de 20% te gaan met de x, dus het feit dat x = 3 betekent dat we nodig hebben 3 liter van de 20%-oplossing. Het uiteindelijke bedrag moest zijn 5 liter. Zodat 2 liter voor de andere, waarbij de 15%-oplossing was verlaat.
- 13Schrijf je je laatste reactie. In dit geval, zouden we schrijven: Hypatia wordt 3 liter van 20%-oplossing en 2 liter van de 15%-oplossing nodig hebben om 5 liter van een 18% oplossing te krijgen.
Dingen die je nodig hebt
- De mogelijkheid op te lossen een eenvoudige algebravergelijking (bijv. 0,20 * x + 0,15 * (1-x) = 0.18)
