Hoe te variantie berekenen

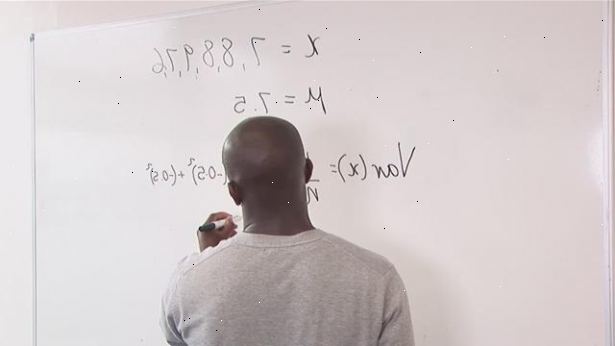
Berekenen van variantie

1. 1
   Noteer de formule voor de berekening van variantie. De formule voor het meten van een onpartijdige schatting van de populatie variantie van een vaste steekproef van n waarnemingen is de volgende: (s ²⁾ = Σ [(x _i - x) ^2] / n - 1. De formule voor het berekenen van de variantie in de hele bevolking is dezelfde als deze behalve de teller n, niet n - 1, maar het moet geen tijd u met een eindige steekproef van waarnemingen worden gebruikt. Hier is wat de onderdelen van de formule voor de berekening van variantie betekenen:
   
   • s ² = Variantie
   • Σ = Sommatie, waarvan de som van elke term in de vergelijking na de sommatie teken betekent.
   • x _i = Sample observatie. Dit vertegenwoordigt elke term in de set.
   • x = De betekenen. Dit vertegenwoordigt het gemiddelde van alle getallen in de reeks.
   • n = De steekproefgrootte. U kunt denken aan dit als het aantal termen in de set.
2. 2
   Bereken de som van de termen. Maak eerst een grafiek die een kolom voor waarnemingen heeft (termen), het gemiddelde (x), de gemiddelde afgetrokken van de termen (x _i - x) en vervolgens het kwadraat van deze voorwaarden [(x _i - x) ^2)]. Nadat u de grafiek hebt gemaakt en geplaatst alle voorwaarden in de eerste kolom, simpelweg optellen van alle nummers in de set. Laten we zeggen dat je werkt met de volgende nummers: 17, 15, 23, 7, 9, 13. Voeg ze gewoon omhoog: 17 + 15 + 23 + 7 + 9 + 13 = 84.
   
3. 3
   Bereken het gemiddelde van de termen. Naar het gemiddelde van een reeks termen vinden, simpelweg optellen van de voorwaarden en het resultaat wordt gedeeld door het aantal termen. In dit geval, weet je al dat de som van de termen is 84. Aangezien er 6 termen, gewoon verdelen 84 met 6 aan de gemiddelde vinden. 84/6 = 14. Schrijf "14" helemaal naar beneden in de kolom voor het gemiddelde.
4. 4
   Trek het gemiddelde van elke term. Aan de derde kolom te vullen, neem dan gewoon elke term uit de steekproef waarnemingen en het aftrekken van 14, het steekproefgemiddelde. U kunt uw werk controleren door het optellen van alle van de resultaten en de bevestiging dat ze optellen tot nul. Hier is hoe elk monster waarneming af te trekken van het gemiddelde:
   • 17-14 = 3
   • 15-14 = 1
   • 23-14 = 9
   • 7-14 = -7
   • 9-14 = -5
   • 13 - 14 = -1
5. 5
   Vierkant elk resultaat. Nu u de gemiddelde hebt afgetrokken van elk monster observatie, gewoon vierkant elk resultaat en schrijf het antwoord in de vierde kolom. Vergeet niet dat al uw resultaten positief zullen zijn. Hier is hoe het te doen:
   • 3 ² = 9
   • 1 ² = 1
   • 9 ² = 81
   • -7 ² = 49
   • -5 ² = 25
   • -1 ² 1 =
6. 6
   Bereken de som van de gekwadrateerde termen. Nu simpelweg optellen van alle nieuwe termen. 9 + 1 + 81 + 49 + 25 + 1 = 166
   
7. 7
   De plaats van de waarden in de oorspronkelijke vergelijking. Sluit gewoon de waarden in de oorspronkelijke vergelijking, eraan te herinneren dat "n" staat voor het aantal datapunten.
   
   • s ² = 166/6-1
8. 8
   Lossen. Gewoon verdelen 166 door 5. Het resultaat is 33.2 Indien u graag om de standaarddeviatie te vinden, gewoon vinden de vierkantswortel van 33.2. √ 33.2 = 5.76. Nu kunt u deze gegevens te interpreteren in een grotere context. Meestal is het verschil tussen twee reeksen gegevens worden vergeleken, en het onderste getal geeft minder variatie binnen die gegevensset.